如圖1，直線GH與直線l1，l2分別交于B，A兩點，點C在直線l2上，射線AD平分∠BAC交直線l1于點E，∠GBE=2∠BAE．
（1）求證：直線l1∥l2；
（2）如圖2，點Q在直線l1上（B點左側），AM平分∠BAQ交l1于點M，過點M作MN⊥AD交AD于點N，請猜想∠BQA與∠AMN的關系；并證明你的結論；
（3）若點P是線段AB上一點，射線EP交直線l2于點F，∠GBE=130°．點N在射線AD上，且滿足∠EBN=∠EFC連接BN，請補全圖形，探究∠BNA與∠FEA滿足的等量關系，并證明．
【考點】平行線的判定與性質．
【答案】（1）見解析；
（2）∠BQA=2∠AMN，見解析；
（3）∠BNA+∠FEA=130°或∠BNA=∠FEA，見解析．
（2）∠BQA=2∠AMN，見解析；
（3）∠BNA+∠FEA=130°或∠BNA=∠FEA，見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/14 1:0:8組卷：517引用：3難度：0.5
相似題
-
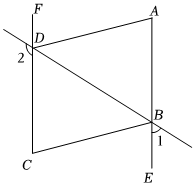1．如圖：已知∠1+∠2=180°，∠A=∠C，BC平分∠DBE．
（1）AE與FC平行嗎？說明理由．
（2）AD與BC的位置關系如何？為什么？
（3）DA平分∠BDF嗎？為什么？發布：2025/5/24 21:0:1組卷：860引用：4難度：0.4 -
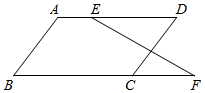2．如圖，AB∥CD，∠B=∠D，直線EF與AD，BC的延長線分別交于點E，F，求證：∠DEF=∠F．發布：2025/5/24 8:30:1組卷：2925引用：34難度：0.7 -
3．【數學抽象】實驗證明：平面鏡反射光線的規律是射到平面鏡上的光線和被反射出的光線與平面鏡所夾的銳角相等，如圖①，一束光線m射到平面鏡a上，被a反射后的光線為n,則入射光線m,反射光線n與平面鏡a所夾的銳角相等，即∠1=∠2．
（1）利用這個規律人們制作了潛望鏡，圖②是潛望鏡工作原理示意圖，AB、CD是平行放置的兩面平面鏡，請解釋進入潛望鏡的光線m為什么和離開潛望鏡的光線n是平行的？
（2）如圖③，改變兩平面鏡之間的位置關系，經過兩次反射后，入射光線m與反射光線n之間的位置關系會隨之改變．若入射光線m與反射光線n平行但方向相反，則兩平面鏡的夾角∠ABC為多少度？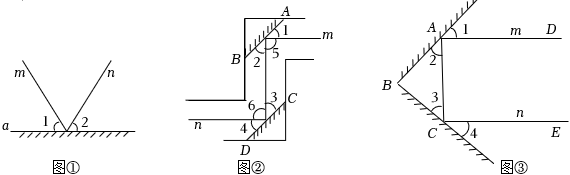
發布：2025/5/24 14:30:1組卷：194引用：3難度：0.8