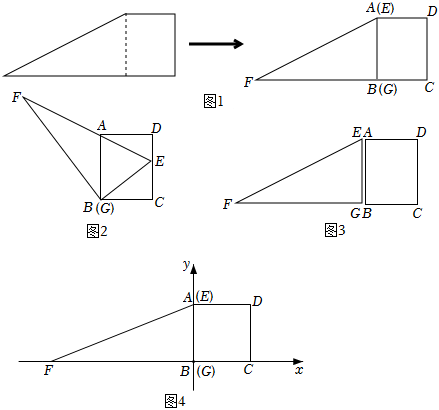
如圖1，小明將一張直角梯形紙片沿虛線剪開，得到矩形和三角形兩張紙片，測得AB=5，AD=4．在進行如下操作時遇到了下列幾個問題，請你幫助解決．
（1）如圖2，將△EFG的頂點G移到矩形的頂點B處，再將三角形繞點B順時針旋轉使E點落在CD邊上，此時EF恰好經過點A，請證明：△ADE∽△FGE；
（2）如圖3，在（1）的條件下，小明先將△EFG的邊EG和矩形的邊AB重合，然后將△EFG沿直線BC向右平移，至F點與B重合時停止．在平移過程中，設G點平移的距離為x,兩紙片重疊部分面積為y,求在平移的整個過程中，y與x的函數關系式．
（3）如圖4，在（1）的條件下，小明把該圖形放在直角坐標系中，使B（G）為坐標原點BC為x軸，在x軸和y上分別找P，Q兩點使△DPQ與△ABF相似，直接寫出P點的坐標．
【考點】相似形綜合題．
【答案】（1）證明過程見解答；
（2）y=
；
（3）P點的坐標為（，0）或（，0）或（-，0）或（-，0）或（-6，0）或（10，0）或（-10，0）或（-26，0）．
（2）y=
- 1 4 x 2 + 5 x （ 0 ≤ x ≤ 4 ） |
- 2 x + 24 （ 4 ＜ x ≤ 10 ） |
（3）P點的坐標為（
3
2
5
2
5
2
7
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：63引用：1難度：0.2
相似題
-
1．綜合與實踐
問題情境：如圖，在Rt△ABC中，∠ACB=90°，將△ABC繞點B順時針旋轉得到Rt△EBD，連接AE，連接CD并延長交AE于點F．
猜想驗證：（1）試猜想△CBD與△ABE是否相似？并證明你的猜想．
探究證明：（2）如圖，連接BF交DE于點H，AB與CF相交于點G，是否成立？并說明理由．DHBH=FHEH
拓展延伸：（3）若CD=EF，直接寫出的值．BCAB發布：2025/5/23 21:30:2組卷：282引用：3難度：0.2 -
2．已知四邊形ABCD中，E、F分別是AB、AD邊上的點，DE與CF交于點G．
問題發現：
（1）①如圖1，若四邊形ABCD是正方形，且DE⊥CF于G，則=；DECF
②如圖2，當四邊形ABCD是矩形時，且DE⊥CF于G，AB=m,AD=n,則=；DECF
拓展研究：
（2）如圖3，若四邊形ABCD是平行四邊形，且∠B+∠EGC=180°時，求證：；DECF=ADCD
解決問題：
（3）如圖4，若BA=BC=5，DA=DC=10，∠BAD=90°，DE⊥CF于G，請直接寫出的值．DECF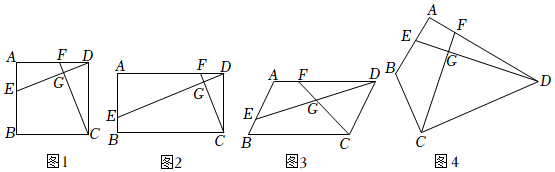
發布：2025/5/23 23:30:1組卷：2292引用：6難度：0.3 -
3．在矩形ABCD中，AB=2，AD=4，F是對角線AC上不與點A，C重合的一點，過F作FE⊥AD于E，將△AEF沿EF翻折得到△GEF，點G在射線AD上，連接CG．
（1）如圖1，若點A的對稱點G落在AD上，∠FGC=90°，延長GF交AB于H，連接CH．
①求證：△CDG∽△GAH；
②求tan∠GHC．
（2）如圖2，若點A的對稱點G落在AD延長線上，∠GCF=90°，判斷△GCF與△AEF是否全等，并說明理由．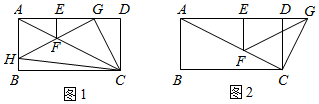
發布：2025/5/23 23:0:1組卷：1132引用：5難度：0.3