“數(shù)形結(jié)合”是一種重要的數(shù)學(xué)思想，八上教材中，我們曾用函數(shù)觀點看方程，也就是利用一次函數(shù)的圖象求解二元一次方程組．類似的，學(xué)習(xí)了一次函數(shù)和反比例函數(shù)之后，我們也可以將方程的解的研究轉(zhuǎn)化為已學(xué)函數(shù)圖象交點的問題…
（1）方程x2-2x-3=0的解可以轉(zhuǎn)化為一次函數(shù)y1和反比例函數(shù)y2的圖象交點問題．請直接寫出一對符合要求的y1和y2的表達式；
（2）利用“數(shù)形結(jié)合”，不解方程，借助下面平面直角坐標(biāo)系，判斷方程x|x-2|=4的解的個數(shù)．
【答案】（1）y1=x-2，y2=；
（2）1個．
3
x
（2）1個．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/2 8:0:8組卷：852引用：1難度：0.5
相似題
-
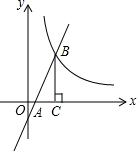1．如圖，一次函數(shù)y=kx-1的圖象與x軸交于點A，與反比例函數(shù)y=（x＞0）的圖象交于點B，BC垂直x軸于點C．若△ABC的面積為1，則k的值是3x．發(fā)布：2025/6/25 6:0:1組卷：1078引用：61難度：0.5 -
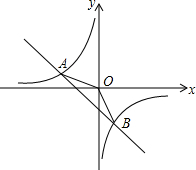2．如圖，在平面直角坐標(biāo)系xOy中，一次函數(shù)y1=ax+b（a,b為常數(shù)，且a≠0）與反比例函數(shù)y2=（m為常數(shù)，且m≠0）的圖象交于點A（-2，1）、B（1，n）．mx
（1）求反比例函數(shù)和一次函數(shù)的解析式；
（2）連接OA、OB，求△AOB的面積；
（3）直接寫出當(dāng)y1＜y2＜0時，自變量x的取值范圍．發(fā)布：2025/6/25 6:0:1組卷：4589引用：75難度：0.5 -
3．反比例函數(shù)y=
（k≠0）與一次函數(shù)y=mx+b（m≠0）交于點A（1，2k-1）．kx
（1）求反比例函數(shù)的解析式；
（2）若一次函數(shù)與x軸交于點B，且△AOB的面積為3，求一次函數(shù)的解析式．發(fā)布：2025/6/25 6:0:1組卷：767引用：63難度：0.5