試卷征集
          
                
          
            
          
            
          
                
          
                    
                    
          加入會員
          
                
          
            
          
            
          
                
          
                    
                    
          操作視頻
          
                
          
            
          
        
          
    
          

    
          
        
    
          
    
          
    
          
        
          
            



          
    
          
        
          
            
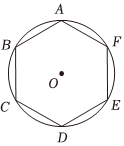
          如圖，設ABCDEF是半徑為1的圓O的內接正六邊形，M是圓O上的動點．
          （1）求
          |
          AB
          +
          BC
          -
          AM
          |
          的最大值；
          （2）求證：
          MA
          2
          +
          MD
          2
          為定值；
          （3）對于平面中的點P，存在實數x與y,使得
          OP
          =
          x
          OE
          +
          y
          OF
          ，若點P是正六邊形ABCDEF內的動點（包含邊界），求x-y的最小值．
          【答案】（1）2；
          （2）4；
          （3）-2．
          【解答】
          【點評】
          聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
          發布：2024/5/28 8:0:9組卷：111引用：1難度：0.6
          
        
          
            
          
                
          相似題
          
                
            
                        
          • 
                            
            1．在△ABC中，已知
            DB
            =
            -
            2
            DC
            ，若向量
            AB
            =
            a
            ，
            AC
            =
            b
            ，則以下各式正確的是（　　）
            發布：2024/12/31 18:30:4組卷：72引用：1難度：0.8
            
                        
            • 
                        
          • 
                            
            2．設D為△ABC所在平面內一點，且滿足
            CD
            =3
            BD
            ，則（　　）
            發布：2024/12/29 13:30:1組卷：167引用：5難度：0.7
            
                        
            • 
                        
          • 
                            
            3．平行四邊形ABCD中，E為AD邊上的中點，連接BE交AC于點G，若
            AG
            =
            λ
            AB
            +
            μ
            AD
            ，則λ+μ=（　　）
            發布：2025/1/5 18:30:5組卷：163引用：2難度：0.7
            
                        
            • 
                
          
            
          
    
          
        

          

        
          
    
          
    
           
        
          APP開發者：深圳市菁優智慧教育股份有限公司| 應用名稱：菁優網 | 應用版本：5.0.7 |隱私協議|第三方SDK|用戶服務條款
          本網部分資源來源于會員上傳，除本網組織的資源外，版權歸原作者所有，如有侵犯版權，請立刻和本網聯系并提供證據，本網將在三個工作日內改正