2022-2023學年上海市楊浦區控江中學高一（下）期末數學試卷

一、填空題（本大題滿分54分）本大概共有12題，1～6題每題4分，7～12題每題5分.

• 1．半徑為2，弧長為2的扇形的圓心角為

  弧度．
  組卷：82引用：1難度：0.9

  解析

• 2．函數y=tanx的最小正周期是

  ．
  組卷：296引用：4難度：0.8

  解析

• 3．向量

  b

  =（3，4）的單位向量

  b

  0

  為

  ．
  組卷：87引用：2難度：0.9

  解析

• 4．若角α的終邊過點P（4，-3），則

  sin

  （

  3

  π

  2

  +

  α

  ）

  =

  ．
  組卷：1223引用：10難度：0.9

  解析

• 5．已知復數z=1+2i,則z?

  z

  =

  ．
  組卷：192引用：8難度：0.7

  解析

• 6．已知直角坐標平面上兩點P₁（-1，1）、P₂（2，3），若P滿足

  P

  1

  P

  =

  2

  P

  P

  2

  ，則點P的坐標為

  ．
  組卷：106引用：1難度：0.7

  解析

• 7．在△ABC中，角A，B，C所對的邊為a,b,c,若a=4，b=6，c=9，則角C=

  ．
  組卷：280引用：2難度：0.8

  解析

三、簡答題（本大題滿分78分）本大題共有5題，解答下列各題必須在答題紙相應編號的規定區域內寫出必得步驟.

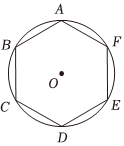• 20．如圖，設ABCDEF是半徑為1的圓O的內接正六邊形，M是圓O上的動點．
  （1）求

  |

  AB

  +

  BC

  -

  AM

  |

  的最大值；
  （2）求證：

  MA

  2

  +

  MD

  2

  為定值；
  （3）對于平面中的點P，存在實數x與y,使得

  OP

  =

  x

  OE

  +

  y

  OF

  ，若點P是正六邊形ABCDEF內的動點（包含邊界），求x-y的最小值．
  組卷：111引用：1難度：0.6

  解析

• 21．設f（z）是一個關于復數z的表達式，若f（x+yi）=x₁+y₁i（其中x,y,x₁，y₁∈R，i為虛數單位），就稱f將點P（x,y）“f對應”到點Q（x₁，y₁）．例如：

  f

  （

  z

  ）

  =

  1

  z

  將點（0，1）“f對應”到點（0，-1）．
  （1）若f（z）=z+1（z∈C），點P₁（1，1）“f對應”到點Q₁，點P₂“對應”到點Q₂（1，1），求點Q₁、P₂的坐標．
  （2）設常數k,t∈R，若直線l：y=kx+t,f（z）=z²（z∈C），是否存在一個有序實數對（k,t），使得直線l上的任意一點P（x,y）“f對應”到點Q（x₁，y₁）后，點Q仍在直線l上？若存在，試求出所有的有序實數對（k,t）；若不存在，請說明理由．
  （3）設常數a,b∈R，集合D{z|z∈C且Rez＞0}和A={w|w∈C且|w|＜1}，若

  f

  （

  z

  ）

  =

  az

  +

  b

  z

  +

  1

  滿足：①對于集合D中的任意一個元素z,都有f（z）∈A；②對于集合A中的任意一個元素w,都存在集合D中的元素z使得w=f（z）．請寫出滿足條件的一個有序實數對（a,b），并論證此時的f（z）滿足條件．
  組卷：72引用：6難度：0.3

  解析