直角三角形兩直角邊的和為17，斜邊長(zhǎng)為13，則這個(gè)直角三角形的面積為3030，斜邊上的高為60136013．
60
13
60
13
【考點(diǎn)】勾股定理．
【答案】30；
60
13
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：30引用：1難度：0.7
相似題
-
1．如圖，在每個(gè)小正方形的邊長(zhǎng)為1的網(wǎng)格中，點(diǎn)A，B，C均在網(wǎng)格的格點(diǎn)上，CD⊥AB于點(diǎn)D，則CD的長(zhǎng)為（ ）發(fā)布：2025/6/5 6:30:2組卷：557引用：2難度：0.6 -
2．定義：若某三角形的三邊長(zhǎng)a,b,c滿足ab+a2=c2，則稱該三角形為“類勾股三角形”．請(qǐng)根據(jù)以上定義解決下列問(wèn)題：
（1）判斷等邊三角形是否為“類勾股三角形”，并說(shuō)明理由；
（2）若等腰三角形ABC是“類勾股三角形”，其中AC=BC，AB＞AC，求∠A的度數(shù)；
（2）如圖，在△ABC中，∠C=2∠A，且∠B＞∠A．證明：△ABC為“類勾股三角形”．發(fā)布：2025/6/5 7:0:2組卷：956引用：8難度：0.4 -
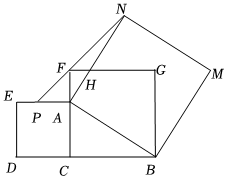3．如圖，在△ABC中，∠ACB=90°，以△ABC的各邊為邊分別作正方形ACDE，正方形BCFG與正方形ABMN，AN與FG相交于點(diǎn)H，連接NF并延長(zhǎng)交AE于點(diǎn)P，且NF=2FP．記△ABC的面積為S1，△FNH的面積為S2，若S2-S1=21，則BC的長(zhǎng)為（ ）發(fā)布：2025/6/5 7:30:1組卷：172引用：2難度：0.4