如圖，在菱形ABCD中，AB=4，按以下步驟作圖：①分別以點C和點D為圓心，大于12CD的長為半徑畫弧，兩弧交于點M，N；②作直線MN，且MN恰好經過點A，與CD交于點E，連接BE，則BE的值為（ ）
1
2
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/2 5:30:2組卷：816引用：14難度：0.5
相似題
-
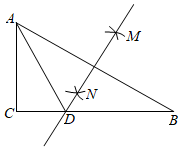1．如圖，在Rt△ABC中，∠C=90°，AC＜BC，分別以頂點A、B為圓心，大于AB的長為半徑作圓弧，兩條圓弧交于點M、N作直線MN交邊CB于點D．若AD=5，CD=3，則AB的長是（ ）12發布：2025/6/3 16:30:1組卷：124引用：7難度：0.5 -
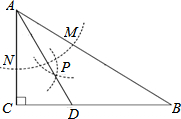2．如圖，在△ABC中，∠C=90°，∠B=30°，以A為圓心，任意長為半徑畫弧分別交AB、AC于點M和N，再分別以M、N為圓心，大于MN的長為半徑畫弧，兩弧交于點P，連接AP并延長交BC于點D，則下列說法中正確的個數是（ ）12
①AD是∠BAC的平分線；
②∠ADC=60°；
③點D在AB的中垂線上．發布：2025/6/3 16:0:1組卷：394引用：10難度：0.9 -
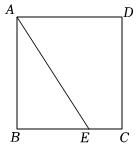3．如圖，在正方形ABCD中，點E在BC上，連接AE．
（1）用尺規完成以下基本作圖：過點D作AE的垂線，分別與AB、AE交于點F、G；（不寫作法和證明，保留作圖痕跡）
（2）在（1）所作的圖形中，求證：AE=DF．（請補全下面的證明過程）
證明：∵四邊形ABCD是正方形，
∴∠ABC=∠BAD=90°，AB=AD．
∵∠BAD=90°，
∴∠BAE+∠DAE=90°．
∵DF⊥AE，
∴∠AGD=．
∴+∠DAE=90°．
又∵∠BAE+∠DAE=90°，
∴．
在△ABE和△DAF中：（），∠ABE=∠DAF（??）∠BAE=∠ADF
∴△ABE≌△DAF（ASA）．
∴AE=DF．發布：2025/6/3 20:30:2組卷：130引用：2難度：0.9