課外興趣小組活動時，老師提出了下面問題：
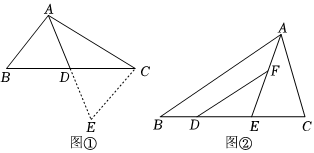
如圖①，AD是△ABC的中線，若AB=3，AC=5，求AD的取值范圍．
“善思小組”通過探究發現，延長AD至點E，使ED=AD，連接CE，可以證出△ADB≌△EDC，利用全等三角形的性質，可將已知的邊長與AD轉化到△ACE中，進而求出AD的取值范圍．
從上面的思路可以看出，解決問題的關鍵是將中線AD延長一倍，構造出全等三角形，我們把這種方法叫做“倍長中線法”．
請你利用“善思小組”的方法思考：
（1）由已知和作圖能得到△ADB≌△EDC的理由是 DD；
A．SSS
B．AAS
C．HL
D．SAS
（2）求得AD的取值范圍是 CC；
A.3＜AD＜5
B.3≤AD≤5
C.1＜AD＜4
D.1≤AD≤4
解題時，條件中若出現“中點”或“中線”字樣，可以考慮延長中線構造全等三角形，把分散的已知條件和所求證的結論集合到同一三角形中．
根據上面解題方法的啟發，請你解答問題．
（3）如圖②，在△ABC中，AB＞AC，點D，E在BC上，點E是CD的中點，DF∥AB交AE于點F，DF=AC．
求證：AE平分∠BAC．
【考點】三角形綜合題．
【答案】D；C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/3 0:0:1組卷：239引用：1難度：0.5
相似題
-
1．如圖1，平面直角坐標系中，A（a,0），B（0，b），C（-1，-3），AC交y軸于D點，BC交x軸于E點，已知
+（b-2）2=0．a-3
（1）求△ABC的面積和D點坐標；
（2）如圖2，M點在x軸上，直線DM交線段AB于N點，若S△BCN=，求M點坐標；178
（3）如圖3，G點在線段OA上，H點在線段AB上，∠BGH=α，∠OBG和∠AHG的平分線交于P點，當∠P變化的過程中，始終有為定值，求α的值．∠OAB∠P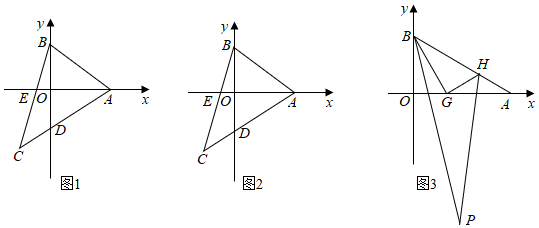
發布：2025/6/22 9:30:1組卷：228引用：1難度：0.1 -
2．如圖，在Rt△ABC中，∠ABC=90°，AC=10cm,BC=8cm,點D是線段AC的中點，動點P從點A出發，沿A-D-B-C向終點C運動，速度為5cm/s,當點P不與點A，B重合時，作PE⊥AB交線段AB于點E，設點P的運動時間為t（s），△APE的面積為S（cm2）．
（1）求AB的長；
（2）當點P在線段BD上時，求PE的長（用含t的式子表示）；
（3）當P沿A-D-B運動時，求S與t之間的函數關系式；
（4）點E關于直線AP的對稱點為E′，當點E′落在△ABC的內部時，直接寫出t的取值范圍．發布：2025/6/22 8:0:2組卷：337引用：3難度：0.3 -
3．已知：如圖①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°．
（1）①求證：AC=BD；
②∠APB=；
（2）如圖②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，則AC與BD間的等量關系為，∠APB的大小為．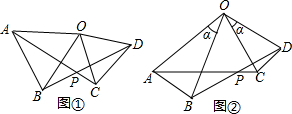
發布：2025/6/22 0:30:2組卷：30引用：1難度：0.5