2023-2024學(xué)年黑龍江省牡丹江市八年級(jí)（上）期中數(shù)學(xué)試卷

一、選擇題（每小題3分，滿分30分）

• 1．中國(guó)文字博大精深，而且有許多是軸對(duì)稱圖形，在這四個(gè)文字中，不是軸對(duì)稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：433引用：29難度：0.9

  解析

• 2．已知△ABC的三條邊分別是a,b,c,化簡(jiǎn)|a-b+c|-|a-b-c|的結(jié)果為（　　）

  A．2a-2b

  B．2a-2c

  C．a(chǎn)-2b

  D．0
  組卷：127引用：3難度：0.5

  解析

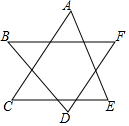• 3．如圖，∠A+∠B+∠C+∠D+∠E+∠F的度數(shù)為（　　）

  A．180°

  B．270°

  C．300°

  D．360°
  組卷：146引用：4難度：0.9

  解析

• 4．下列條件中能判定△ABC≌△DEF的是（　　）

  A．AB=DE，BC=EF，∠A=∠D	B．∠A=∠D，∠B=∠E，∠C=∠F
  C．AC=DF，∠B=∠F，AB=DE	D．∠B=∠E，∠C=∠F，AC=DF
  組卷：2793引用：33難度：0.7

  解析

• 5．具備下列條件的三角形中，不是直角三角形的是（　　）

  A．∠A+∠B=∠C

  B．∠B=∠C= 1 2 ∠A

  C．∠A-∠B=90°

  D．∠A=90°-∠B
  組卷：136引用：5難度：0.5

  解析

• 6．一個(gè)多邊形截去一個(gè)角后，形成另一個(gè)多邊形的內(nèi)角和為720°，那么原多邊形的邊數(shù)為（　　）

  A．5

  B．5或6

  C．6或7

  D．5或6或7
  組卷：877引用：7難度：0.7

  解析

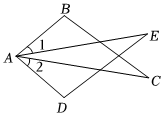• 7．如圖，已知∠B=∠D，AB=AD，添加下列條件：①AC=AE；②∠1=∠2；③BC=DE；④∠C=∠E中的一個(gè)，能使△ABC≌△ADE的條件有（　　）

  A．4個(gè)

  B．3個(gè)

  C．2個(gè)

  D．1個(gè)
  組卷：16引用：1難度：0.5

  解析

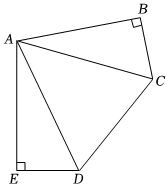• 8．如圖，在五邊形ABCDE中，∠B=∠E=90°，

  ∠

  CAD

  =

  1

  2

  ∠

  BAE

  ，AB=AE，且CD=4，AE=3，則五邊形ABCDE的面積為（　　）

  A．6

  B．8

  C．10

  D．12
  組卷：40引用：1難度：0.9

  解析

三、解答題（滿分60分）

• 24．課外興趣小組活動(dòng)時(shí)，老師提出了下面問題：
  如圖①，AD是△ABC的中線，若AB=3，AC=5，求AD的取值范圍．
  “善思小組”通過探究發(fā)現(xiàn)，延長(zhǎng)AD至點(diǎn)E，使ED=AD，連接CE，可以證出△ADB≌△EDC，利用全等三角形的性質(zhì)，可將已知的邊長(zhǎng)與AD轉(zhuǎn)化到△ACE中，進(jìn)而求出AD的取值范圍．
  從上面的思路可以看出，解決問題的關(guān)鍵是將中線AD延長(zhǎng)一倍，構(gòu)造出全等三角形，我們把這種方法叫做“倍長(zhǎng)中線法”．
  請(qǐng)你利用“善思小組”的方法思考：
  （1）由已知和作圖能得到△ADB≌△EDC的理由是

  ；
  A．SSS
  B．AAS
  C．HL
  D．SAS
  （2）求得AD的取值范圍是

  ；
  A.3＜AD＜5
  B.3≤AD≤5
  C.1＜AD＜4
  D.1≤AD≤4
  解題時(shí)，條件中若出現(xiàn)“中點(diǎn)”或“中線”字樣，可以考慮延長(zhǎng)中線構(gòu)造全等三角形，把分散的已知條件和所求證的結(jié)論集合到同一三角形中．
  根據(jù)上面解題方法的啟發(fā)，請(qǐng)你解答問題．
  （3）如圖②，在△ABC中，AB＞AC，點(diǎn)D，E在BC上，點(diǎn)E是CD的中點(diǎn)，DF∥AB交AE于點(diǎn)F，DF=AC．
  求證：AE平分∠BAC．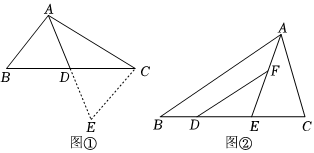
  
  組卷：239引用：1難度：0.5

  解析

• 25．探究式學(xué)習(xí)是新課程倡導(dǎo)的重要學(xué)習(xí)方法，某數(shù)學(xué)興趣小組擬做以下探究．
  如圖，在△ABC中，BD、CE分別是AC、AB上的高，點(diǎn)G在直線CE上，CG=AB，點(diǎn)F在直線BD上，BF=AC，F(xiàn)N⊥BC于點(diǎn)N，GM⊥BC于點(diǎn)M．探究線段BC，F(xiàn)N，GM之間的數(shù)量關(guān)系．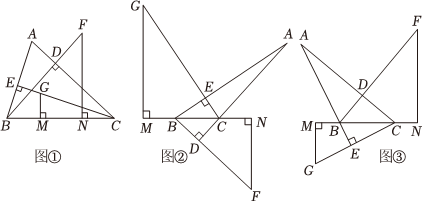
  
  （1）如圖①，當(dāng)△ABC是銳角三角形時(shí)，線段BC，F(xiàn)N，GM之間的數(shù)量關(guān)系是

  ．
  “善思小組”通過探究后發(fā)現(xiàn)解決此問題的方法：過點(diǎn)A作AP⊥BC于點(diǎn)P，利用全等三角形的性質(zhì)進(jìn)而得證．請(qǐng)你寫出證明過程．
  下面是小強(qiáng)的部分證明過程，仔細(xì)閱讀并完成相應(yīng)的任務(wù)．
  

  證明：過點(diǎn)A作AP⊥BC于點(diǎn)P． ∴∠APB=90°． ∴∠BAP+∠ABP=90°． ∵CE⊥AB， ∴∠BCE+∠ABP=90°． ∴∠BAP=∠BCE． ∵GM⊥BC， ∴∠CMG=90°．

  ∴∠APB=∠CMG=90°． 在△APB和△CMG中， ∵∠BAP=∠GCM， ∠APB=∠CMG，AB=CG， ∴△APB≌△CMG（AAS）． ∴BP=GM．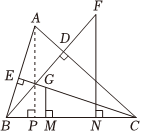

  請(qǐng)你補(bǔ)全余下的證明過程．
  （2）通過類比、轉(zhuǎn)化、猜想，探究出：當(dāng)△ABC是鈍角三角形，且AB＞AC時(shí)，如圖②線段BC，F(xiàn)N，GM之間的數(shù)量關(guān)系是

  ；當(dāng)△ABC是鈍角三角形，且AB＜AC時(shí)，如圖③，線段BC，F(xiàn)N，GM之間的數(shù)量關(guān)系是

  ．
  （3）“智慧小組”繼續(xù)對(duì)上述問題進(jìn)行特殊化研究后，提出下面問題請(qǐng)你解答：
  在（1）和（2）的條件下，若MN=2BC=8，CD：AD=1：3，則S_△BCD=

  ．
  組卷：66引用：1難度：0.4

  解析