在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E．
（1）當直線MN繞點C旋轉到圖1的位置時，求證：
①△ADC≌△CEB；
②DE=AD+BE；
（2）當直線MN繞點C旋轉到圖2的位置時，AD=5，BE=2，求線段DE的長．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。

發(fā)布：2024/10/18 0:0:1組卷：2992引用：11難度：0.3

相似題

1．如圖，O是正△ABC內一點，OA=3，OB=4，OC=5，將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′，下列結論：①△BO′A可以由△BOC繞點B逆時針旋轉60°得到；②點O與O′的距離為4；③∠AOB=150°；④S_{四邊形AOBO′}=6+3
3
；⑤S_△AOC+S_△AOB=6+
9
4
3
．其中正確的結論是（　　）
A．①②③⑤ B．①②③④ C．①②③④⑤ D．①②③
發(fā)布：2025/6/4 17:0:1組卷：11504引用：43難度：0.3
解析
2．如圖，一個含有30°角的三角板ABC，繞點B順時針旋轉到A′BC′的位置，使A，B，C′在同一條直線上，則旋轉角的度數(shù)為
．
發(fā)布：2025/6/4 15:0:1組卷：266引用：7難度：0.7
解析
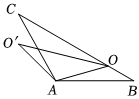3．如圖，在△ABC中，∠BAC=120°，AB=AC=6，O為BC邊上一動點，連接AO，將線段AO繞點A逆時針旋轉120°至AO′，則線段OO′的最小值為
．
發(fā)布：2025/6/4 17:0:1組卷：339引用：3難度：0.6
解析

相關試卷

在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E．（1）當直線MN繞點C旋轉到圖1的位置時，求證：①△ADC≌△CEB；②DE=AD+BE；（2）當直線MN繞點C旋轉到圖2的位置時，AD=5，BE=2，求線段DE的長．