為滿足市場需求，某超市在新年來臨前夕，購進一款商品，每盒進價是40元．超市規定每盒售價不得少于45元．根據以往銷售經驗發現；當售價定為每盒45元時，每天可以賣出700盒，如果每盒售價每提高1元，則每天要少賣出20盒．
（1）試求出每天的銷售量y（盒）與每盒售價x（元）之間的函數關系式；
（2）要使每天銷售的利潤為6000元，且讓顧客得到最大的實惠．售價應定為多少元？
（3）當每盒售價定為多少元時，每天銷售的利潤P（元）最大？最大利潤是多少？
【答案】（1）每天的銷售量y（盒）與每盒售價x（元）之間的函數關系式為y=-20x+1600（45≤x＜80）；（2）售價應定為50元；（3）每盒售價定為60元時，每天銷售的利潤P（元）最大，最大利潤是8000元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/12/6 22:30:1組卷：1259引用：8難度：0.4
相似題
-
1．周長是4m的矩形，它的面積S（m2）與一邊長x（m）的函數圖象大致是（ ）
發布：2025/5/28 4:30:1組卷：1057引用：5難度：0.5 -
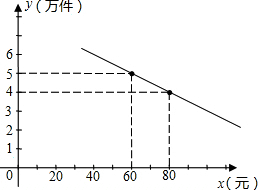2．某通訊器材公司銷售一種市場需求較大的新型通訊產品．已知每件產品的進價為40元，每年銷售該種產品的總開支（不含進價）總計120萬元．在銷售過程中發現，年銷售量y（萬件）與銷售單價x（元）之間存在著如圖所示的一次函數關系．
（1）求y關于x的函數關系式；
（2）試寫出該公司銷售該種產品的年獲利z（萬元）關于銷售單價x（元）的函數關系式（年獲利=年銷售額一年銷售產品總進價一年總開支）．當銷售單價x為何值時，年獲利最大并求這個最大值；
（3）若公司希望該種產品一年的銷售獲利不低于40萬元，借助（2）中函數的圖象，請你幫助該公司確定銷售單價的范圍．在此情況下，要使產品銷售量最大，你認為銷售單價應定為多少元？發布：2025/5/28 3:0:1組卷：415引用：44難度：0.1 -
3．我市某企業生產的一批產品上市后40天內全部售完，該企業對這一批產品上市后每天的銷售情況進行了跟蹤調查．表一、表二分別是國內、國外市場的日銷售量y1、y2（萬件）與時間t（t為整數，單位：天）的部分對應值．
表一：國內市場的日銷售情況
表二：國外市場的日銷售情況時間t（天） 0 1 2 10 20 30 38 39 40 日銷售量y1（萬件） 0 5.85 11.4 45 60 45 11.4 5.85 0
（1）請你從所學過的一次函數、二次函數和反比例函數中確定哪種函數能表示y1與t的變化規律，寫出y1與t的函數關系式及自變量t的取值范圍；時間t（天） 0 1 2 3 25 29 30 31 32 33 39 40 日銷售量y2（萬件） 0 2 4 6 50 58 60 54 48 42 6 0
（2）分別探求該產品在國外市場上市30天前與30天后（含30天）的日銷售量y2與時間t所符合的函數關系式，并寫出相應自變量t的取值范圍；
（3）設國內、外市場的日銷售總量為y萬件，寫出y與時間t的函數關系式．試用所得函數關系式判斷上市后第幾天國內、外市場的日銷售總量y最大，并求出此時的最大值．發布：2025/5/28 2:0:5組卷：175引用：14難度：0.6