如圖，矩形ABCD中，AB=3，BC=2，點M在BC上，連接AM，作∠AMN=∠AMB，點N在直線AD上，MN交CD于點E．
（1）求證：△AMN是等腰三角形；
（2）求證：AM2=2BM?AN；
（3）當M為BC中點時，求ME的長．
【考點】相似形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：746引用：6難度：0.3
相似題
-
1．（1）閱讀解決
華羅庚是我國著名的數學家，他推廣的優選法，就是以黃金分割法為指導，用最可能少的試驗次數，盡快找到生產和科學實驗中最優方案的一種科學試驗方法．
黃金分割是指將整體一分為二，較大部分與整體部分的比值等于較小部分與較大部分的比值，這個比例被公認為最能引起美感的比例，因此被稱為黃金分割．
如圖①，點B把線段AC分成兩部分，如果=BCAB，那么稱點B為線段AC的黃金分割點，它們的比值為ABAC．5-12
在圖①中，若AB=12m,則BC的長為 cm；
（2）問題解決
如圖②，用邊長為40m的正方形紙片進行如下操作：對折正方形ABCD得折痕EF，連接CE，將CB折疊到CE上，點B對應點為H，折痕為CG．
證明：G是AB的黃金分割點；
（3）拓展探究
如圖③在邊長為m的正方形ABCD的邊AD上任取點E（AE＞DE），連接BE，作CF⊥BE，交AB于點F，延長EF，CB交于點P．發現當PB與BC滿足某種關系時，E、F恰好分別是AD、AB的黃金分割點．請猜想這一發現，并說明理由，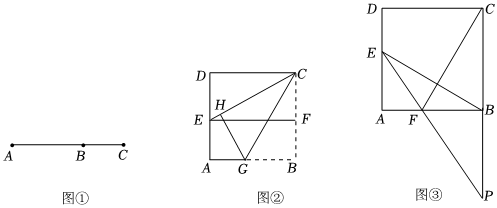
發布：2025/5/25 8:0:2組卷：188引用：1難度：0.3 -
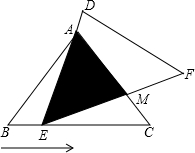2．如圖，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，將△DEF與△ABC重合在一起，△ABC不動，△DEF運動，并滿足：點E在邊BC上沿B到C的方向運動，且DE始終經過點A，EF與AC交于M點．
（1）求證：△ABE∽△ECM；
（2）當DE⊥BC時，
①求CM的長；
②直接寫出重疊部分的面積；
（3）在△DEF運動過程中，當重疊部分構成等腰三角形時，求BE的長．發布：2025/5/25 10:30:1組卷：659引用：3難度：0.2 -
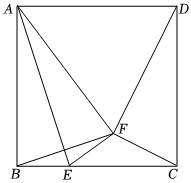3．已知正方形ABCD中，AB=a.E是BC邊上一點（不與B，C重合），BE=b,連接AE，作點B關于AE的對稱點F．連接AF，BF，CF，DF．
（1）求∠BFD的度數．
（2）當△DFC是直角三角形時，求證：BF是CF和DF的比例中項．
（3）在（2）的條件下，求tan∠FDC以及a：b的值．發布：2025/5/25 9:0:1組卷：249引用：1難度：0.3