已知數軸上三點M，O，N對應的數分別為-2，0，4，點P為數軸上任意一點，其對應的數為x.
（1）如果點P到點M，點N的距離相等，那么x的值是 11．
（2）數軸上是否存在點P，使點P到點M，點N的距離之和是9？若存在，請求出x的值；若不存在，請說明理由．
（3）如果點P以每秒2個單位長度的速度從點O向右運動時，點M和點N分別以每秒1個單位長度和每秒3個單位長度的速度向左運動，且三點同時出發，那么幾秒時點P到點M，點N的距離相等？
【答案】1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 3:30:2組卷：405引用：2難度：0.5
相似題
-
1．在數軸上A，B兩點對應的數字分別為-2和10，點P從點A出發，以每秒3個單位長度的速度向右運動，同時點Q從點B出發，以每秒1個單位長度的速度向左運動，設它們的運動時間為t秒．當PQ=6時，求t的值．發布：2025/6/4 20:0:1組卷：128引用：1難度：0.6 -
2．某中學組織一批學生春游，原計劃租用45座客車若干輛，但有15人沒有座位；若租用同樣數量的60座客車，則多出一輛車，且其余客車恰好坐滿．已知45座客車租金為每輛300元，60座客車租金為每輛400元，問：
（1）這批學生的人數是多少？原計劃租用多少輛45座客車？
（2）若租用同一種車，要使每位學生都有座位，應該怎樣租用才合算？發布：2025/6/4 20:30:1組卷：1140引用：5難度：0.7 -
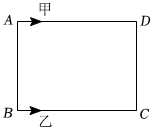3．如圖，甲、乙兩位同學在長方形場地ABCD上繞著四周跑步，甲沿著A-D-C-B-A方向循環跑步，同時乙沿著B-C-D-A-B方向循環跑步，AB=30米，BC=50米，若甲速度為2米/秒，乙速度3米/秒．
（1）設經過的時間為t秒，則用含t的代數式表示甲的路程為 米；
（2）當甲、乙兩人第一次相遇時，求所經過的時間t為多少秒？
（3）若甲改為沿著A-B-C-D-A的方向循環跑步，而乙仍按原來的方向跑步，兩人的速度不變，求經過多少秒，乙追上甲？
（4）在（3）的條件下，當乙第一次追上甲后繼續跑步，則最少再經過a秒乙又追上甲，這時兩人所處的位置在點P；直接寫出a的值，在圖中標出點P，不要求書寫過程．發布：2025/6/4 19:0:1組卷：271引用：2難度：0.5