現(xiàn)將連續(xù)自然數(shù)1至2009按圖中的方式排列成一個(gè)長方形隊(duì)列，再用正方形任意框出16個(gè)數(shù)．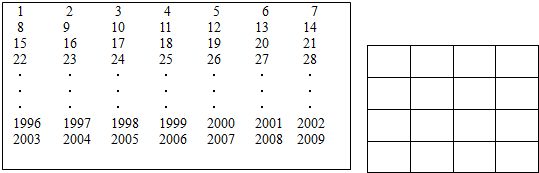
（1）設(shè)任意一個(gè)這樣的正方形框中的最小數(shù)為n,請用n的代數(shù)式表示該框中的16個(gè)數(shù)，然后填入右表中相應(yīng)的空格處，并求出這16個(gè)數(shù)中的最小數(shù)nn和最大數(shù)n+24n+24，然后填入右表中相應(yīng)的空格處，并求出這16個(gè)數(shù)的和16（n+12）16（n+12）．（用n的代數(shù)式表示）
（2）在圖中，要使一個(gè)正方形框出的16個(gè)數(shù)之和分別等于832、2000、2008是否可能？若不可能，請說明理由；若可能，請求出該正方形框出的16個(gè)數(shù)中的最小數(shù)和最大數(shù)．
（3）計(jì)算出該長方形隊(duì)列中，共可框出多少個(gè)這樣不同的正方形框？
【考點(diǎn)】規(guī)律型：數(shù)字的變化類．
【答案】n；n+24；16（n+12）
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：144引用：5難度：0.5
相似題
-
1．已知
，Tn（x）=f1（x）+f2（x）+f3（x）+…+fn（x）（n為正整數(shù)），下列說法：fn（x）=nx1+x
①；fn（2023）+fn（12023）=n
②；f1（1）f1（11）+f2（2）f2（12）+f3（3）f3（13）+?+fn（n）fn（1n）=n2+n
③；Tn-1（x）Tn（x）＞nn+1
④若，則y的最小值為3．y=1+ttft（t）-Tt（t）+3
其中正確選項(xiàng)的個(gè)數(shù)是（ ）發(fā)布：2025/5/22 23:30:1組卷：635引用：4難度：0.3 -
2．觀察下列數(shù)據(jù)：
，-12，25，-310，417，…，則第12個(gè)數(shù)是（ ）526發(fā)布：2025/5/23 1:0:1組卷：1183引用：9難度：0.6 -
3．按一定規(guī)律排列的一組數(shù)據(jù)：
，12，-35，12，-717，926，…．則按此規(guī)律排列的第10個(gè)數(shù)是 ．-1137發(fā)布：2025/5/23 0:0:1組卷：277引用：1難度：0.5
相關(guān)試卷