解題方法回顧：
在求某邊上的高之類問題時(shí)，常常利用同一個(gè)圖形面積不變或等底等高面積不變或多個(gè)圖形面積之和不變的原理來解決，稱為“等積法”．
解題方法應(yīng)用：
（1）已知：如圖1，矩形ABCD中，AB=5，BC=12，對(duì)角線AC、BD相交于點(diǎn)O，點(diǎn)P是線段AD上任意一點(diǎn)，且PE⊥AC于點(diǎn)E，PF⊥BD于點(diǎn)F，求PE+PF的值．
小陳同學(xué)想到了利用“等積法”解決本題，過程如下：（如圖2）
解：連接PO，∵矩形ABCD的兩邊AB=5，BC=12，
∴S矩形ABCD=AB?BC=60，OA=OC，OB=OD，AC=BD，
∴AC=AB2+BC2=122+52=13，
∴S△AOD=14S矩形ABCD=15，OA=OD=12AC=132，
∴S△AOD=S△AOP+S△DOP=12OA?PE+12OD?PF=12OA（PE+PF）=12×132×（PE+PF）=15，
∴PE+PF=60136013．（請(qǐng)你填上小陳計(jì)算的正確答案）
（2）如圖3，正方形ABCD的邊長(zhǎng)為2，點(diǎn)P為邊BC上任意一點(diǎn)（可與B點(diǎn)或C點(diǎn)重合），分別過B、C、D作射線AP的垂線，垂足分別是B'，C'，D'．
①設(shè)AP=x,BB'+CC'+DD'=y,求y與x的函數(shù)關(guān)系式，并求出x取值范圍；
②直接寫出y的最大值為 44，最小值為 2222
AC
=
A
B
2
+
B
C
2
=
12
2
+
5
2
=
13
S
△
AOD
=
1
4
S
矩形
ABCD
=
15
OA
=
OD
=
1
2
AC
=
13
2
S
△
AOD
=
S
△
AOP
+
S
△
DOP
=
1
2
OA
?
PE
+
1
2
OD
?
PF
=
1
2
OA
（
PE
+
PF
）
1
2
×
13
2
×
（
PE
+
PF
）
=
15
60
13
60
13
2
2
【考點(diǎn)】四邊形綜合題．
【答案】；4；2
60
13
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：424引用：3難度：0.4
相似題
-
1．如圖，將矩形紙片ABCD沿對(duì)角線AC折疊，使點(diǎn)B落在點(diǎn)E處，AE交CD于點(diǎn)F，且已知AB=8，BC=4．
（1）判斷△ACF的形狀，并說明理由；
（2）求△ACF的面積；
（3）點(diǎn)P為AC上一動(dòng)點(diǎn)，則PE+PF最小值為．發(fā)布：2025/6/8 19:30:1組卷：143引用：2難度：0.3 -
2．按要求回答下列問題：
發(fā)現(xiàn)問題．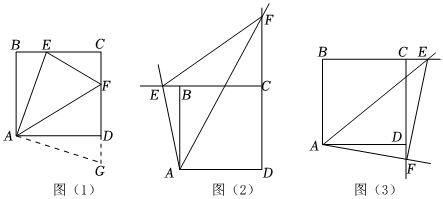
（1）如圖（1），在正方形ABCD中，點(diǎn)E，F(xiàn)分別是BC，CD邊上的動(dòng)點(diǎn)，且∠EAF=45°，易證：EF=DF+BE．（不必證明）；
（2）類比延伸
①如圖（2），在正方形ABCD中，如果點(diǎn)E，F(xiàn)分別是邊BC，CD延長(zhǎng)線上的動(dòng)點(diǎn)，且∠EAF=45°，則（1）中的結(jié)論還成立嗎？請(qǐng)寫出證明過程；
②如圖（3），如果點(diǎn)E，F(xiàn)分別是邊BC，CD延長(zhǎng)線上的動(dòng)點(diǎn)，且∠EAF=45°，則EF，BE，DF之間的數(shù)量關(guān)系是 ．（不要求證明）
（3）拓展應(yīng)用：如圖（1），若正方形的ABCD邊長(zhǎng)為6，，求EF的長(zhǎng)．AE=35發(fā)布：2025/6/8 18:30:1組卷：235引用：4難度：0.1 -
3．在矩形ABCD中，AB=3，BC=8，F(xiàn)是BC邊上的中點(diǎn)，動(dòng)點(diǎn)E在邊AD上，連接EF，過點(diǎn)F作FP⊥EF分別交射線AD、射線CD于點(diǎn)P、Q．
（1）如圖1，當(dāng)點(diǎn)P與點(diǎn)Q重合時(shí)，求PF的長(zhǎng)；
（2）如圖2，當(dāng)點(diǎn)Q在線段CD上（不與C，D重合）且tanP=時(shí)，求AE的長(zhǎng)；12
（3）線段PF將矩形分成兩個(gè)部分，設(shè)較小部分的面積為y,AE長(zhǎng)為x,求y與x的函數(shù)關(guān)系式．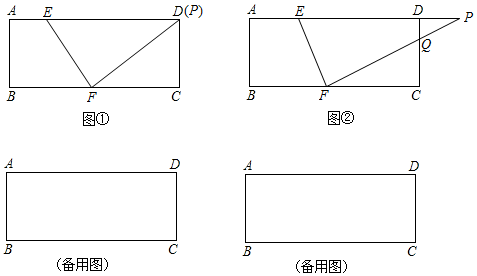
發(fā)布：2025/6/8 19:0:1組卷：200引用：2難度：0.3