2021年新冠肺炎仍在世界好多國家肆虐，并且出現了傳染性更強的“德爾塔”變異毒株、“拉姆達”變異毒株，盡管我國抗疫取得了很大的成績，疫情也得到了很好的遏制，但由于整個國際環境的影響，時而也會出現一些散發病例，故而抗疫形勢依然艱巨，日常防護依然不能有絲毫放松．在日常防護中，口罩是必不可少的防護用品．某口罩生產廠家為保障抗疫需求，調整了口罩生產規模．已知該廠生產口罩的固定成本為200萬元，每生產x萬箱，需另投入成本p（x）萬元，當年產量不足90萬箱時，p（x）=12x2+40x；當年產量不低于100萬箱時，p（x）=100x+8lnx+760x-2180，若每萬箱口罩售價100萬元，通過市場分析，該口罩廠生產的口罩當年可以全部銷售完．
（1）求年利潤y（萬元）關于年產量x（萬箱）的函數關系式；
（2）年產量為多少萬箱時，該口罩生產廠家所獲得年利潤最大？（注：ln95≈4.55）
1
2
760
x
【考點】利用導數研究函數的單調性；根據實際問題選擇函數類型．
【答案】（1）
；（2）年產量為95萬箱．
y
=
- 1 2 x 2 + 60 x - 200 ， 0 ＜ x ＜ 90 |
1980 - 8 lnx - 760 x ， x ≥ 90 |
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：77引用：8難度：0.6
相似題
-
1．已知函數f（x）=x3-2kx2+x-3在R上不單調，則k的取值范圍是 ；
發布：2024/12/29 13:0:1組卷：236引用：3難度：0.8 -
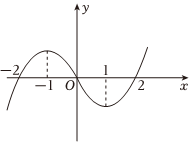2．在R上可導的函數f（x）的圖象如圖示，f′（x）為函數f（x）的導數，則關于x的不等式x?f′（x）＜0的解集為（ ）發布：2024/12/29 13:0:1組卷：265引用：7難度：0.9 -
3．已知函數f（x）=ax2+x-xlnx（a∈R）
（Ⅰ）若函數f（x）在（0，+∞）上單調遞增，求實數a的取值范圍；
（Ⅱ）若函數f（x）有兩個極值點x1，x2（x1≠x2），證明：．x1?x2＞e2發布：2024/12/29 13:30:1組卷：143引用：2難度：0.2