問題背景:
在△ABC中,AB、BC、AC三邊的長分別為5、10、13,求這個三角形的面積.
小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),然后在網格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處,AB=22+12=5,BC=10,AC=13),如圖①所示.這樣不需求△ABC的高,而借用網格就能計算出它的面積.這種求△ABC面積的方法叫做構圖法.
(1)請你將△ABC的面積直接填寫在橫線上:3.53.5.
思維拓展:
(2)若△ABC三邊的長分別為5a、22a、17a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
探索創新:
(3)若△ABC三邊的長分別為m2+16n2、9m2+4n2、2m2+n2(m>0,n>0,且m≠n),求這個三角形的面積.
(4)直接寫出當x為何值時,函數y=x2+9+(12-x)2+4有最小值,最小值是多少?

5
10
13
2
2
+
1
2
5
10
13
5
2
17
m
2
+
16
n
2
9
m
2
+
4
n
2
m
2
+
n
2
x
2
+
9
(
12
-
x
)
2
+
4
【答案】3.5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/16 12:0:1組卷:282引用:2難度:0.3
相似題
-
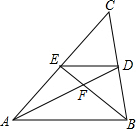 1.如圖,在△ABC中,AD,BE是兩條中線,則△EFD和△BFA的面積之比是( )
1.如圖,在△ABC中,AD,BE是兩條中線,則△EFD和△BFA的面積之比是( )A.1:2 B.1:4 C.1:3 D.2:3 發布:2025/6/3 3:30:2組卷:658引用:3難度:0.5 -
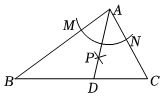 2.小明用尺規在△ABC上作圖,并留下如圖所示的痕跡,若AB=6,AC=4,則△ABD與△ACD的面積之比為( )
2.小明用尺規在△ABC上作圖,并留下如圖所示的痕跡,若AB=6,AC=4,則△ABD與△ACD的面積之比為( )A.3:2 B.9:4 C.9:2 D.3:1 發布:2025/6/3 10:30:2組卷:290引用:4難度:0.8 -
3.一定能將三角形的面積分成相等的兩部分的是三角形的( )
A.高線 B.中線 C.角平分線 D.都不是 發布:2025/6/3 7:30:2組卷:212引用:7難度:0.9


