綜合與實踐
[問題情境]學習完《解直角三角形的應用》后,同學們對如何建立解直角三角形的模型測量物體的實際高度產生了濃厚的興趣,數學老師決定開展一次主題為《測量學校旗桿高度》的數學實踐活動,并為各小組準備了卷尺、測角儀等工具,要求各小組建立測高模型并測量學校旗桿的高度.
[問題探究]第一小組的同學經過討論,制定出了如下測量實施方案:
第一步,建立測高模型,畫出測量示意圖(如圖1),明確需要測量的數據和測量方法:用卷尺測量測角儀CD的高度和測角儀底部C與旗桿底部A之間的距離,用測角儀測量旗桿頂端B的仰角α;
第二步,進行組員分工,制作測量數據記錄表;
第三步,選擇不同的位置測量三次,依次記錄測量數據;
第四步,整理數據,計算旗桿的高,撰寫研究報告.
如表是該組同學研究報告中的數據記錄和計算結果:
| 測量組別 | CD的長(米) | AC的長(米) | 仰角α | 計算AB的高(米) |
| 位置1 | 1 | 14.4 | 40° | 13.1 |
| 位置2 | 1 | 16.2 | 36° | 12.8 |
| 位置3 | 1 | 15.9 | 38° | 13.4 |
| 平均值 | 13.1 | |||
| 研究結論:旗桿的高為n米 | ||||
13.1
13.1
;該小組選擇不同的位置測量三次,再以三次測量計算的旗桿高度的平均數作為研究結論,這樣做的目的是 減小誤差
減小誤差
.(2)該測量模型中,若CD=a,AC=b,仰角為α,用含a,b,α的代數式表示旗桿AB的高度為
btanα+a
btanα+a
.[拓展應用]
(3)第二小組同學設計的是另外一種測量方案,他們畫出的測量示意圖如圖2,測量時,固定測角儀的高度為1m,先在點C處測得旗桿頂端B的仰角α=30°,然后朝旗桿方向前進14m到達點H處,再次測得旗桿頂端B的仰角β=60°,請你幫他們求出旗桿AB的高度(結果保留根號).

【考點】解直角三角形的應用-仰角俯角問題;列代數式.
【答案】13.1;減小誤差;btanα+a
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:360引用:3難度:0.4
相似題
-
1.我國航天事業捷報頻傳,天舟二號于2021年5月29日成功發射,震撼人心.當天舟二號從地面到達點A處時,在P處測得A點的仰角∠DPA為30°且A與P兩點的距離為6千米,它沿鉛垂線上升7.5秒后到達B處,此時在P處測得B點的仰角∠DPB為45°,求天舟二號從A處到B處的平均速度.(結果精確到1m/s,取
=1.732,3=1.414)2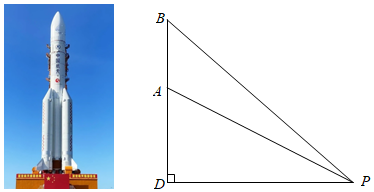 發布:2025/5/26 10:0:1組卷:963引用:12難度:0.5
發布:2025/5/26 10:0:1組卷:963引用:12難度:0.5 -
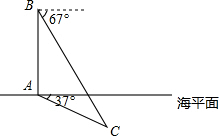 2.在某次反潛演習中,我軍艦A測得離開海平面的下潛潛艇C的俯角為37°,位于軍艦A正上方1100米的反潛飛機B測得此時潛艇C的俯角為67°,求前艇C離海平面的下潛深度.(參考數據:sin37°≈,cos37°≈35,tan37°≈45,sin67°≈34,cos67°≈1213,tan67°≈513)125發布:2025/5/26 10:30:2組卷:243引用:2難度:0.7
2.在某次反潛演習中,我軍艦A測得離開海平面的下潛潛艇C的俯角為37°,位于軍艦A正上方1100米的反潛飛機B測得此時潛艇C的俯角為67°,求前艇C離海平面的下潛深度.(參考數據:sin37°≈,cos37°≈35,tan37°≈45,sin67°≈34,cos67°≈1213,tan67°≈513)125發布:2025/5/26 10:30:2組卷:243引用:2難度:0.7 -
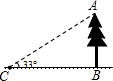 3.(Ⅰ)如圖,從點C測得樹的頂端的仰角為33°,BC=20米,則樹高AB=米(用計算器計算,結果精確到0.1米).
3.(Ⅰ)如圖,從點C測得樹的頂端的仰角為33°,BC=20米,則樹高AB=米(用計算器計算,結果精確到0.1米).
(Ⅱ)計算:sin30°?cos30°-tan30°=(結果保留根號).發布:2025/5/28 6:30:1組卷:37引用:1難度:0.7
相關試卷


