某公司全年圓滿完成預定的生產任務，為答謝各位員工一年來的銳意進取和辛勤努力，公司決定在聯(lián)歡晚會后，擬通過摸球兌獎的方式對500位員工進行獎勵，規(guī)定：每位員工從一個裝有4種面值的獎券的箱子中，一次隨機摸出2張獎券，獎券上所標的面值之和就是該員工所獲得的獎勵額．
（1）若箱子中所裝的4種面值的獎券中有1張面值為80元，其余3張均為40元，試比較員工獲得80元獎勵額與獲得120元獎勵額的概率的大小；
（2）公司對獎勵總額的預算是6萬元，預定箱子中所裝的4種面值的獎券有兩種方案：第一方案是2張面值20元和2張面值100元；第二方案是2張面值40元和2張面值80元．為了使員工得到的獎勵總額盡可能地符合公司的預算且每位員工所獲得的獎勵額相對均衡，請問選擇哪一種方案比較好？并說明理由．
【答案】（1）相等；
（2）第二種方案．
第一種方案為（20，20，100，100），
設員工所獲得的獎勵額為X1，則X1的分布列為
所以X1的數(shù)學期望為，
X1的方差為；
第二種方案為（40，40，80，80），
設員工所獲得的獎勵額為X2，則X2的分布列為
所以X2的數(shù)學期望為，
X2的方差為，
又因為500E（X1）=500E（X2）=60000（元），
所以兩種方案獎勵額的數(shù)學期望都符合要求，但第二種方案的方差比第一種方案的小，
（2）第二種方案．
第一種方案為（20，20，100，100），
設員工所獲得的獎勵額為X1，則X1的分布列為
| X1 | 40 | 120 | 200 |
| P | 1 6 |
2 3 |
1 6 |
E
（
X
1
）
=
40
×
1
6
+
120
×
2
3
+
200
×
1
6
=
120
X1的方差為
D
（
X
1
）
=
（
40
-
120
）
2
×
1
6
+
（
120
-
120
）
2
×
2
3
+
（
200
-
120
）
2
×
1
6
=
6400
3
第二種方案為（40，40，80，80），
設員工所獲得的獎勵額為X2，則X2的分布列為
| X2 | 80 | 120 | 160 |
| P | 1 6 |
2 3 |
1 6 |
E
（
X
2
）
=
80
×
1
6
+
120
×
2
3
+
160
×
1
6
=
120
X2的方差為
D
（
X
2
）
=
（
80
-
120
）
2
×
1
6
+
（
120
-
120
）
2
×
2
3
+
（
160
-
120
）
2
×
1
6
=
1600
3
又因為500E（X1）=500E（X2）=60000（元），
所以兩種方案獎勵額的數(shù)學期望都符合要求，但第二種方案的方差比第一種方案的小，
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：287引用：6難度：0.5
相似題
-
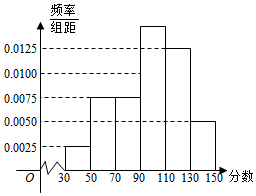1．某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規(guī)定：初賽成績大于90分的具有復賽資格，某校有800名學生參加了初賽，所有學生的成績均在區(qū)間（30，150]內，其頻率分布直方圖如圖．
（Ⅰ）求獲得復賽資格的人數(shù)；
（Ⅱ）從初賽得分在區(qū)間（110，150]的參賽者中，利用分層抽樣的方法隨機抽取7人參加學校座談交流，那么從得分在區(qū)間（110，130]與（130，150]各抽取多少人？
（Ⅲ）從（Ⅱ）抽取的7人中，選出3人參加全市座談交流，設X表示得分在區(qū)間（130，150]中參加全市座談交流的人數(shù)，求X的分布列及數(shù)學期望E（X）．發(fā)布：2024/12/29 13:30:1組卷：133引用：7難度：0.5 -
2．設離散型隨機變量X的分布列如表：
若離散型隨機變量Y=-3X+1，且E（X）=3，則（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 發(fā)布：2024/12/29 13:0:1組卷：198引用：6難度：0.5 -
3．從4名男生和2名女生中任選3人參加演講比賽，用X表示所選3人中女生的人數(shù)，則E（X）為（ ）
發(fā)布：2024/12/29 13:30:1組卷：138引用：6難度：0.7