【閱讀理解】
數形結合是解決數學問題的一種重要的思想方法,借助這種方法可將抽象的數學知識變得直觀起來并且具有可操作性,從而可以幫助我們進行推理,獲得結論.初中數學里的一些代數公式,很多都可以借助幾何圖形進行直觀推導和解釋.
例如:求1+2+3+4+…+n的值(其中n是正整數).
如果采用數形結合的方法,即用圖形的性質來說明數量關系的事實,那就非常的直觀.現利用圖形的性質來求1+2+3+4+…+n的值,方案如下:如圖1,斜線左邊的三角形圖案是由上到下每層依次分別為1,2,3,…,n個小圓圈排列組成的.而組成整個三角形小圓圈的個數恰為所求式子1+2+3+4+…+n的值.為求式子的值,現把左邊三角形倒放于斜線右邊,與原三角形組成一個平行四邊形.此時,組成平行四邊形的小圓圈共有n行,每行有(n+1)個小圓圈,所以組成平行四邊形小圓圈的總個數為n(n+1)個,因此,組成一個三角形小圓圈的個數為n(n+1)2,即1+2+3+4+?+n=n(n+1)2.
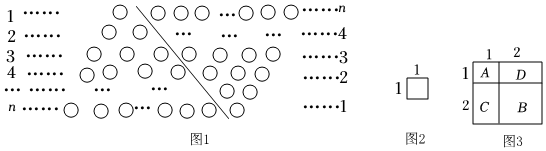
【問題提出】
求13+23+33+?+n3的值(其中n是正整數).
【問題解決】
為解決上述問題,我們借鑒已有的經驗,采用由特殊到一般,歸納的研究方法,利用數形結合法,借助圖形進行推理獲得結論.
探究1
如圖2,13可以看成1個1×1的正方形的面積,即13=1×12=12.
探究2
如圖3,A表示1個1×1的正方形,其面積為:1×12=13;B表示1個2×2的正方形,其面積為:1×22;C,D分別表示1個1×2的長方形,其面積的和為:2×1×2=1×22;B,C,D的面積和為1×22+1×22=(1+1)×22=23,而A,B,C,D恰好可以拼成一個(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32.
探究3
請你類比上述探究過程,借助圖形探究:13+23+33=(1+2+3)2(1+2+3)2=6262.(要求自己構造圖形并寫出推證過程)
【結論歸納】
將上述探究過程發現的規律,推廣到一般情況中去,通過歸納,我們便可以得到:13+23+33+?+n3=(1+2+3+???+n)2(1+2+3+???+n)2=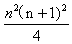
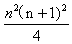 .(要求直接寫出結論,不必寫出推證過程)
.(要求直接寫出結論,不必寫出推證過程)
【結論應用】
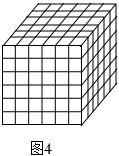
圖4是由若干個棱長為1的小正方體搭成的大正方體,圖中大小正方體一共有多少個?
為了準確數出大小正方體的總個數,我們可以分類統計,即數出棱長分別是1,2,3,4,5,6的正方體的個數,再求總和.
例如:棱長是1的正方體有:6×6×6=63個,
棱長是2的正方體有:5×5×5=53個,
…
棱長是6的正方體有:1×1×1=13個;
然后利用上面歸納的結論,通過計算,可得圖4中大小正方體的個數為 441441.
【逆向應用】
如果由若干個棱長為1的小正方體搭成的大正方體中,大小正方體一共有36100個,那么棱長為1的小正方體的個數為 68596859.
【拓展探究】
觀察下列各式:13=1;23=3+5;33=7+9+11;43=13+15+17+19;??
若m3(m為正整數)按上面規律展開后,發現等式右邊含有“2021”這個數,則m的值 m≥45m≥45.
n
(
n
+
1
)
2
n
(
n
+
1
)
2
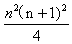
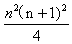
【答案】(1+2+3)2;62;(1+2+3+???+n)2;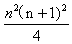 ;441;6859;m≥45
;441;6859;m≥45
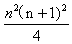 ;441;6859;m≥45
;441;6859;m≥45【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:560引用:1難度:0.3
相似題
-
1.已知a=2002x+2003,b=2002x+2004,c=2002x+2005,則多項式a2+b2+c2-ab-bc-ca的值為( )
A.0 B.1 C.2 D.3 發布:2025/5/28 0:30:1組卷:6234引用:40難度:0.7 -
2.滿足方程x3+6x2+5x=27y3+9y2+9y+1的正整數對(x,y)有( )
A.0對 B.1對 C.3對 D.無數對 發布:2025/5/28 1:0:2組卷:177引用:2難度:0.7 -
3.計算
=( )11×3+12×4+13×5+…+118×20A. 531380B. 1062380C. 2940D. 531760發布:2025/5/28 0:30:1組卷:333引用:1難度:0.7


