2022年山東省青島市李滄區中考數學二模試卷

一、選擇題：本大題共8小題，每小題3分，共24分.

• 1．下列品牌的標識中，是軸對稱圖形但不是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：115引用：3難度：0.9

  解析

• 2．-5的絕對值是（　　）

  A． 1 5

  B．5

  C．-5

  D．- 1 5
  組卷：282引用：328難度：0.9

  解析

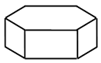• 3．如圖所示的正六棱柱的主視圖是（　　）

  A．

  B．

  C．

  D．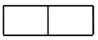
  組卷：690引用：10難度：0.9

  解析

• 4．月球與地球之間的平均距離約為38.4萬公里，38.4萬用科學記數法表示為（　　）

  A．38.4×104

  B．3.84×105

  C．0.384×106

  D．3.84×106
  組卷：321引用：8難度：0.9

  解析

• 5．在平面直角坐標系中，將線段AB平移后得到線段A'B'，點A（2，2）的對應點A'的坐標為（-2，-2），則點B（-1，1）的對應點B'的坐標為（　　）

  A．（5，3）

  B．（1，-1）

  C．（-5，-3）

  D．（4，5）
  組卷：230引用：6難度：0.8

  解析

• 6．下列運算中，正確的是（　　）

  A．a2?a5=a10	B．（a-b）2=a2-b2
  C．（-3a3）2=6a6	D．-3a2b+2a2b=-a2b
  組卷：1326引用：30難度：0.5

  解析

• 7．如圖，在Rt△ABC中，∠ABC=90°，AB=4

  3

  ，BC=4，以AB的中點O為圓心，OA的長為半徑作圓，交AC于點D，則圖中陰影部分的面積為（　　）

  A． 5 3 - 2 π

  B． 5 3 + 2 π

  C． 4 3 - π

  D． 4 3 + π
  組卷：480引用：2難度：0.5

  解析

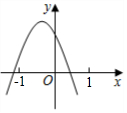• 8．已知二次函數y=ax²+bx+c的圖象如圖所示，則一次函數y=bx+c的圖象和反比例函數y=

  a

  +

  b

  +

  c

  x

  的圖象在同一坐標系中大致為（　　）

  A．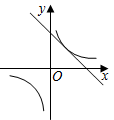

  B．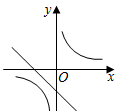

  C．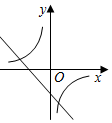

  D．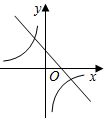
  組卷：1684引用：17難度：0.6

  解析

四、解答題：本大題共9小題，共74分.

• 23．【閱讀理解】
  數形結合是解決數學問題的一種重要的思想方法，借助這種方法可將抽象的數學知識變得直觀起來并且具有可操作性，從而可以幫助我們進行推理，獲得結論．初中數學里的一些代數公式，很多都可以借助幾何圖形進行直觀推導和解釋．
  例如：求1+2+3+4+…+n的值（其中n是正整數）．
  如果采用數形結合的方法，即用圖形的性質來說明數量關系的事實，那就非常的直觀．現利用圖形的性質來求1+2+3+4+…+n的值，方案如下：如圖1，斜線左邊的三角形圖案是由上到下每層依次分別為1，2，3，…，n個小圓圈排列組成的．而組成整個三角形小圓圈的個數恰為所求式子1+2+3+4+…+n的值．為求式子的值，現把左邊三角形倒放于斜線右邊，與原三角形組成一個平行四邊形．此時，組成平行四邊形的小圓圈共有n行，每行有（n+1）個小圓圈，所以組成平行四邊形小圓圈的總個數為n（n+1）個，因此，組成一個三角形小圓圈的個數為

  n

  （

  n

  +

  1

  ）

  2

  ，即1+2+3+4+?+n=

  n

  （

  n

  +

  1

  ）

  2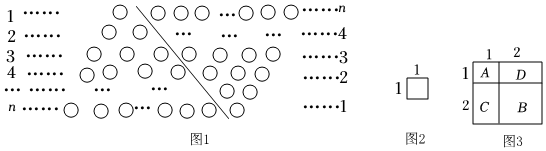

  ．
  
  【問題提出】
  求1³+2³+3³+?+n³的值（其中n是正整數）．
  【問題解決】
  為解決上述問題，我們借鑒已有的經驗，采用由特殊到一般，歸納的研究方法，利用數形結合法，借助圖形進行推理獲得結論．
  探究1
  如圖2，1³可以看成1個1×1的正方形的面積，即1³=1×1²=1²．
  探究2
  如圖3，A表示1個1×1的正方形，其面積為：1×1²=1³；B表示1個2×2的正方形，其面積為：1×2²；C，D分別表示1個1×2的長方形，其面積的和為：2×1×2=1×2²；B，C，D的面積和為1×2²+1×2²=（1+1）×2²=2³，而A，B，C，D恰好可以拼成一個（1+2）×（1+2）的大正方形．
  由此可得：1³+2³=（1+2）²=3²．
  探究3
  請你類比上述探究過程，借助圖形探究：1³+2³+3³=

  =

  ．（要求自己構造圖形并寫出推證過程）
  【結論歸納】
  將上述探究過程發現的規律，推廣到一般情況中去，通過歸納，我們便可以得到：1³+2³+3³+?+n³=

  =

  ．（要求直接寫出結論，不必寫出推證過程）
  【結論應用】
  圖4是由若干個棱長為1的小正方體搭成的大正方體，圖中大小正方體一共有多少個？
  為了準確數出大小正方體的總個數，我們可以分類統計，即數出棱長分別是1，2，3，4，5，6的正方體的個數，再求總和．
  例如：棱長是1的正方體有：6×6×6=6³個，
  棱長是2的正方體有：5×5×5=5³個，
  …
  棱長是6的正方體有：1×1×1=1³個；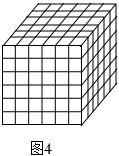
  
  然后利用上面歸納的結論，通過計算，可得圖4中大小正方體的個數為

  ．
  【逆向應用】
  如果由若干個棱長為1的小正方體搭成的大正方體中，大小正方體一共有36100個，那么棱長為1的小正方體的個數為

  ．
  【拓展探究】
  觀察下列各式：1³=1；2³=3+5；3³=7+9+11；4³=13+15+17+19；??
  若m³（m為正整數）按上面規律展開后，發現等式右邊含有“2021”這個數，則m的值

  ．
  組卷：559引用：1難度：0.3

  解析

• 24．已知：線段EF和矩形ABCD如圖①擺放（點E與點B重合），點F在邊BC上，EF=1cm,AB=4cm,BC=8cm.如圖②，EF從圖①的位置出發，沿BC方向運動，速度為1cm/s；動點P同時從點D出發，沿DA方向運動，速度為1cm/s.點M為AB的中點，連接PM，ME，DF，PM與AC相交于點Q，設運動時間為t（s）（0＜t≤7）．
  解答下列問題：
  
  （1）當PM⊥AC時，求t的值；
  （2）設五邊形PMEFD的面積為S（cm²），求S與t的關系式；
  （3）當ME∥AC時，求線段AQ的長；
  （4）當t為何值時，五邊形DAMEF的周長最小，最小是多少？（直接寫出答案即可）
  組卷：334引用：4難度：0.2

  解析