垃圾是人類日常生活和生產(chǎn)中產(chǎn)生的廢棄物,由于排出量大,成分復雜多樣,且具有污染性,所以需要無害化、減量化處理.某市為調查產(chǎn)生的垃圾數(shù)量,采用簡單隨機抽樣的方法抽取20個縣城進行了分析,得到樣本數(shù)據(jù)(xi,yi)(i=1,2,?,20),其中xi和yi分別表示第i個縣城的人口(單位:萬人)和該縣年垃圾產(chǎn)生總量(單位:噸),并計算得20∑i=1xi=80,20∑i=1yi=4000,20∑i=1(xi-x)2=80,20∑i=1(yi-y)2=8000,20∑i=1(xi-x)(yi-y)=700.
(1)請用相關系數(shù)說明該組數(shù)據(jù)中y與x之間的關系可用線性回歸模型進行擬合;
(2)求y關于x的線性回歸方程;
(3)某科研機構研發(fā)了兩款垃圾處理機器,其中甲款機器每臺售價100萬元,乙款機器每臺售價80萬元,下表是以往兩款垃圾處理機器的使用年限統(tǒng)計表:
20
∑
i
=
1
x
i
=
80
20
∑
i
=
1
y
i
=
4000
20
∑
i
=
1
(
x
i
-
x
)
2
=
80
20
∑
i
=
1
(
y
i
-
y
)
2
=
8000
20
∑
i
=
1
(
x
i
-
x
)
(
y
i
-
y
)
=
700
| 1年 | 2年 | 3年 | 4年 | 合計 | |
| 甲款 | 5 | 20 | 15 | 10 | 50 |
| 乙款 | 15 | 20 | 10 | 5 | 50 |
參考公式:相關系數(shù)
r
=
n
∑
i
=
1
(
x
i
-
x
)
(
y
i
-
y
)
n
∑
i
=
1
(
x
i
-
x
)
2
n
∑
i
=
1
(
y
i
-
y
)
2
?
y
=
?
b
x
+
?
a
?
b
=
n
∑
i
=
1
(
x
i
-
x
)
(
y
i
-
y
)
n
∑
i
=
1
(
x
i
-
x
)
2
?
a
=
y
-
?
b
x
【答案】(1)因為y與x的相關系數(shù)接近1,所以y與x之間具有較強的線性相關關系,可用線性回歸模型進行擬合;(2);(3)甲款.
?
y
=
8
.
75
x
+
165
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:197引用:1難度:0.4
相似題
-
 1.某科研機構為了了解氣溫對蘑菇產(chǎn)量的影響,隨機抽取了某蘑菇種植大棚12月份中5天的日產(chǎn)量y(單位:kg)與該地當日的平均氣溫x(單位:℃)的數(shù)據(jù),得到如圖散點圖:
1.某科研機構為了了解氣溫對蘑菇產(chǎn)量的影響,隨機抽取了某蘑菇種植大棚12月份中5天的日產(chǎn)量y(單位:kg)與該地當日的平均氣溫x(單位:℃)的數(shù)據(jù),得到如圖散點圖:
其中A(3,2),B(5,10),C(8,11),D(9,13),E(10,14).
(1)求出y關于x的線性回歸方程;
(2)若該地12月份某天的平均氣溫為6℃,用(1)中所求的回歸方程預測該蘑菇種植大棚當日的產(chǎn)量.
附:線性回歸直線方程中,?y=?bx+?a,?b=n∑i=1xiyi-nxyn∑i=1x2i-nx2.?a=y-?bx發(fā)布:2024/12/29 11:30:2組卷:104引用:3難度:0.7 -
2.兩個線性相關變量x與y的統(tǒng)計數(shù)據(jù)如表:
其回歸直線方程是x 9 9.5 10 10.5 11 y 11 10 8 6 5 =?yx+40,則相應于點(9,11)的殘差為 .?b發(fā)布:2024/12/29 12:0:2組卷:115引用:8難度:0.7 -
3.某農(nóng)科所對冬季晝夜溫差(最高溫度與最低溫度的差)大小與某反季節(jié)大豆新品種一天內發(fā)芽數(shù)之間的關系進行了分析研究,他們分別記錄了12月1日至12月6日每天晝夜最高、最低的溫度(如圖1),以及實驗室每天每100顆種子中的發(fā)芽數(shù)情況(如圖2),得到如下資料:
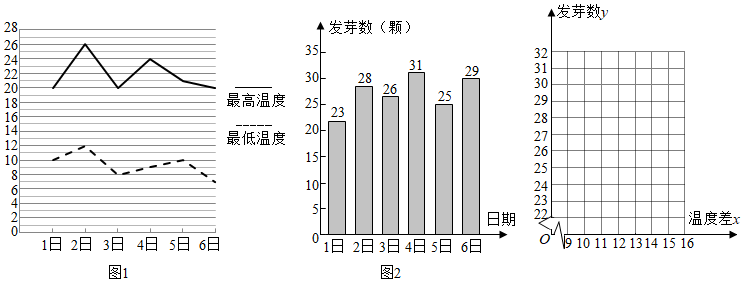
(1)請畫出發(fā)芽數(shù)y與溫差x的散點圖;
(2)若建立發(fā)芽數(shù)y與溫差x之間的線性回歸模型,請用相關系數(shù)說明建立模型的合理性;
(3)①求出發(fā)芽數(shù)y與溫差x之間的回歸方程(系數(shù)精確到0.01);?y=?a+?bx
②若12月7日的晝夜溫差為8℃,通過建立的y關于x的回歸方程,估計該實驗室12月7日當天100顆種子的發(fā)芽數(shù).
參考數(shù)據(jù):=2051,6∑i=1xi=75,6∑i=1yi=162,6∑i=1xiyi≈4.2,6∑i=1xi2-6x2≈6.5.6∑i=1yi2-6y2
參考公式:
相關系數(shù):r=(當|r|>0.75時,具有較強的相關關系).n∑i=1xiyi-nx?y(n∑i=1xi2-nx2)(n∑i=1yi2-ny2)
回歸方程中斜率和截距計算公式:?y=?a+?bx=?b,n∑i=1xiyi-nx?yn∑i=1xi2-nx2=?ay-?b.x發(fā)布:2024/12/29 12:0:2組卷:188引用:5難度:0.5


