在矩形ABCD中，AB=3，AD=5，經過折疊使點A落在BC邊上的點E處，折痕為PQ．當點E在BC邊上移動時，折痕的端點P，Q也隨之移動．規定點P、Q分別在AB，AD上移動．
（1）當點A落在圖1中E點處，如果PA=2，求BE的長為多少？
（2）當點E恰好是BC的中點時，AP和DQ的長分別是多少？
（3）點E在BC邊上可移動的最大距離是多少？
【考點】四邊形綜合題．
【答案】（1）BE的長為；
（2）當點E恰好是BC的中點時，AP=，DQ=；
（3）點E在BC邊上可移動的最大距離是2．
3
（2）當點E恰好是BC的中點時，AP=
61
24
39
20
（3）點E在BC邊上可移動的最大距離是2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 19:30:2組卷：70引用：2難度：0.1
相似題
-
1．如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角平分線CF于點F．
（1）求證：AE=EF；
（2）如圖2，若把條件“點E是邊BC的中點”改為“點E是邊BC上的任意一點”，其余條件不變，（1）中的結論是否仍然成立？；（填“成立”或“不成立”）；
（3）如圖3，若把條件“點E是邊BC的中點”改為“點E是邊BC延長線上的一點”，其余條件仍不變，那么結論AE=EF是否成立呢？若成立請證明，若不成立說明理由．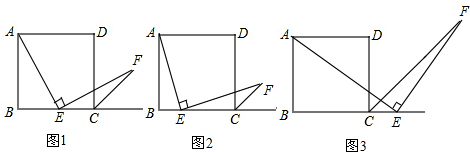
發布：2025/6/8 3:0:2組卷：677引用：7難度：0.5 -
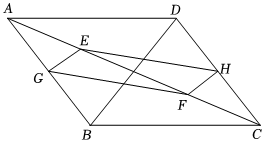2．已知菱形ABCD的邊長為2cm,∠B=120°，E、F為對角線AC上的兩個動點，分別從A、C同時出發，相向而行，速度均為1cm/s,運動時間為t秒，0≤t≤6．3
（1）直接寫出EF的長 （用含t的式子表示）；
（2）若G，H分別為AB，DC的中點，t≠3，求證：四邊形EGFH始終為平行四邊形；
（3）在（2）的條件下，當四邊形EGFH為矩形時，求t的值．發布：2025/6/8 2:30:2組卷：110引用：1難度：0.2 -
3．如圖1，在正方形ABCD中，點E是BC邊上的一點，∠AEP=90°，且EP交正方形外角的平分線CP于點P．
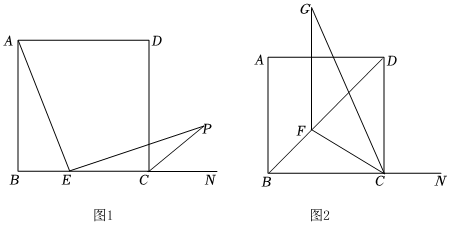
（1）求∠ECP的度數；
（2）求證：AE=EP；
（3）在AB邊上是否存在點M，使得四邊形DEPM是平行四邊形？若存在，請畫出圖形并給予證明；若不存在，請說明理由；
（4）如圖2，在邊長為4的正方形ABCD中，將線段AB沿射線BD平移，得到線段GF，連接CG、CF則直接寫出CF+CG的最小值是 ．發布：2025/6/8 3:30:1組卷：41引用：1難度：0.2