如圖，在四面體OABC中，M是棱OA上靠近A的三等分點，N，P分別是BC，MN的中點，設(shè)h→OA=h→a，h→OB=h→b，h→OC=h→c，用h→a，h→b，h→c表示h→OP，則（ ）
h→
OA
=
h→
a
h→
OB
=
h→
b
h→
OC
=
h→
c
h→
a
h→
b
h→
c
h→
OP
【考點】空間向量基底表示空間向量．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：278引用：9難度：0.6
相似題
-
1．17世紀(jì)，笛卡爾在《幾何學(xué)》中，通過建立坐標(biāo)系，引入點的坐標(biāo)的概念，將代數(shù)對象與幾何對象建立關(guān)系，從而實現(xiàn)了代數(shù)問題與幾何問題的轉(zhuǎn)化，打開了數(shù)學(xué)發(fā)展的新局面，創(chuàng)立了新分支——解析幾何．我們知道，方程x=1在一維空間中表示一個點；在二維空間中，它表示一條直線；在三維空間中，它表示一個平面．那么，過點P0（1，2，1）且以
=（-2，1，3）為法向量的平面的方程為（ ）h→μ發(fā)布：2024/10/23 6:0:3組卷：90引用：4難度：0.8 -
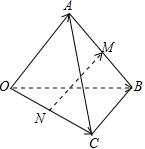2．三棱錐O-ABC中，M，N分別是AB，OC的中點，且=h→OA，h→a=h→OB，h→b=h→OC，用h→c，h→a，h→b表示h→c，則h→NM等于（ ）h→NM發(fā)布：2024/12/17 2:30:1組卷：2295引用：19難度：0.9 -
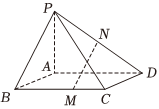3．四棱錐P-ABCD底面ABCD為平行四邊形，M，N分別為棱BC，PD上的點，，PN=ND，設(shè)CMCB=13，h→AB=h→a，h→AD=h→b，則向量h→AP=h→c用基底h→MN表示為（ ）{h→a，h→b，h→c}
?發(fā)布：2024/10/25 4:0:2組卷：434引用：6難度：0.7