（1）【嘗試與感悟】如圖1，在?ABCD中，用圓規和無刻度的直尺在AD上求作一點E，使得點E為AD的中點；
（2）如圖2，在?ABCD中，E為AD的中點，連接EC，點D與點D′關于EC對稱，連接AD′并延長交BC于點G，請判斷BG與ED的數量關系，并加以證明．
（3）【遷移與應用】如圖3，在菱形ABCD中，∠B=60°，點M為邊AB上一動點（M與A、B不重合），連接MC，將△BMC沿著MC所在的直線翻折，得到△B′MC；
①已知AB=4，若B′C⊥BC，求△B′MC與菱形ABCD重合部分的面積；
②設∠BCM=α，CB′與AD的交點為H，當點H在以點C為圓心，MC為半徑的圓上，求α的值．
【考點】圓的綜合題．
【答案】（1）作圖見解析過程；
（2）DE=GB，證明見解析過程；
（3）①；
②40°．
（2）DE=GB，證明見解析過程；
（3）①
36
-
18
3
②40°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/2 8:0:8組卷：72引用：2難度：0.5
相似題
-
1．如圖①，已知⊙O是△ABC的外接圓，∠ABC=∠ACB=α（45°＜α＜90°，D為
上一點，連接CD交AB于點E．?AB
（1）連接BD，若∠CDB=40°，求α的大小；
（2）如圖②，若點B恰好是中點，求證：CE2=BE?BA；?CD
（3）如圖③，將CD分別沿BC、AC翻折得到CM、CN，連接MN，若CD為直徑，請問是否為定值，如果是，請求出這個值，如果不是，請說明理由．ABMN
發布：2025/5/23 23:30:1組卷：1566引用：4難度：0.3 -
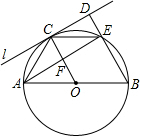2．如圖，AB為⊙O的直徑，C為半圓上一動點，過點C作⊙O的切線l,過點B作BD⊥l,垂足為D，BD與⊙O交于點E，連接OC，CE，AE，AE交OC于點F．
（1）求證：△CDE≌△EFC；
（2）若AB=4，連接AC．
①當AC=時，四邊形OBEC為菱形；
②當AC=時，四邊形EDCF為正方形．發布：2025/5/23 23:30:1組卷：963引用：8難度：0.5 -
3．【問題提出】
（1）如圖①，在Rt△ABC中，∠A=90°，AB=3，AC=4，點D是邊BC上一動點，DE⊥AB于點E，DF⊥AC于點F，則EF的最小值為 ．
【問題探究】
（2）如圖②，在△ABC中，∠A=45°，AB=4，AC=3，點D是BC邊上一動點，DE⊥AB于點E，DF⊥AC于點F，⊙O是四邊形AEDF的外接圓，求⊙O直徑的最小值．2
【問題解決】
（3）某小區內有一塊形狀為四邊形的空地，如圖③所示，在四邊形ABCD中，AD∥BC，∠C=90°，∠B=60°，AD=200米，AB=4003米，點E在CD上，且CE=2DE，F、G分別是邊AB、BC上的兩個動點，且∠FEG=60°．為了改善人居環境，小區物業準備在盡可能大的四邊形BFEG區域內種植花卉，請問這個四邊形BFEG區域的面積是否存在最大值？若存在，求出面積的最大值；若不存在，請說明理由．3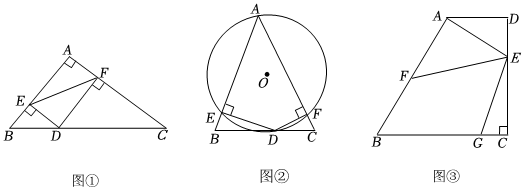
發布：2025/5/24 0:30:1組卷：570引用：3難度：0.1