定義：若一個四邊形能被其中的一條對角線分割成兩個相似三角形，則稱這個四邊形為“師梅四邊形”，這條對角線稱為“師梅線”．我們熟知的平行四邊形就是“師梅四邊形”．
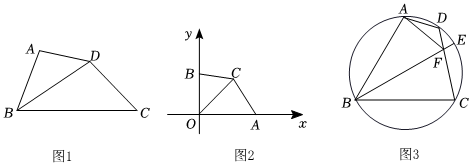
（1）如圖1，BD平分∠ABC，BD=42，BC=10．四邊形ABCD是被BD分割成的“師梅四邊形”，求AB長；
（2）如圖2，平面直角坐標系中，A、B分別是x軸和y軸上的點，且OA=3，OB=2，若點C是直線y=x在第一象限上的一點，且OC是四邊形OACB的“師梅線”，求四邊形OACB的面積；
（3）如圖3，圓內接四邊形ABCD中，∠ABC=60°，點E是?AC的中點，連接BE交CD于點F，連接AF，∠DAF=30°，
①求證：四邊形ABCF是“師梅四邊形”；
②若△ABC的面積為63，求線段BF的長．
BD
=
4
2
?
AC
6
3
【考點】圓的綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1172引用：9難度：0.1
相似題
-
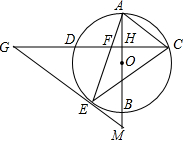1．如圖，AB是⊙O的直徑，弦CD⊥AB，垂足為H，連接AC，過上一點E作EG∥AC交CD的延長線于點G，連接AE交CD于點F，且EG=FG，連接CE．?BD
（1）求證：△ECF∽△GCE；
（2）求證：EG是⊙O的切線；
（3）延長AB交GE的延長線于點M，若tan∠G=，AH=3，求EM的值．34發布：2025/5/23 5:30:3組卷：2325引用：12難度：0.1 -
2．如圖1，⊙O為等腰三角形ABC的外接圓，AB=AC，點D在
上，連結CD，點E為DA延長線上一點，連結CE交⊙O于點F，滿足?AB=2?BC，連結AF．?DF
（1）求證：CE⊥DE；
（2）當，且∠DCB=50°時，求?AF=2?AD的值；AEEF
（3）如圖2，連結DF交AC于點G，若DF=30，⊙O的半徑為25，
①求BC的長；
②當DF∥BC時，直接寫出△AGF與△AEC的面積之比．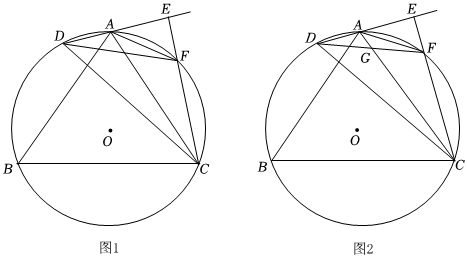
發布：2025/5/23 6:0:2組卷：421引用：1難度：0.1 -
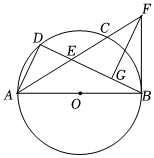3．如圖，AB是⊙O直徑，點C為劣弧中點，弦AC、BD相交于點E，點F在AC的延長線上，EB=FB，FG⊥DB，垂足為G．?BD
（1）求證：∠ABD=∠BFG；
（2）求證：BF是⊙O的切線；
（3）當時，求tan∠DAE的值．DEEG=23發布：2025/5/23 5:30:3組卷：535引用：4難度：0.5