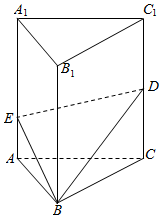
如圖，三棱柱ABC-A1B1C1中，平面ABC⊥平面AA1C1C，AB⊥AC，AA1=AB=AC=2，∠AAC=60°，過AA1的平面交B1C1于點(diǎn)E，交BC于點(diǎn)F．
（Ⅰ）求證：A1C⊥平面ABC1；
（Ⅱ）求證：四邊形AA1EF為平行四邊形；
（Ⅲ）若BFBC=23，求二面角B-AC1-F的大小．
BF
BC
=
2
3
【考點(diǎn)】空間向量法求解二面角及兩平面的夾角；直線與平面垂直．
【答案】（Ⅰ）證明過程見解答；（Ⅱ）證明過程見解答；（Ⅲ）45°．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/20 8:0:8組卷：45引用：1難度：0.5
相似題
-
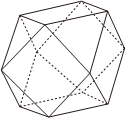1．“阿基米德多面體”也稱為半正多面體，是由邊數(shù)不全相同的正多邊形為面圍成的多面體，它體現(xiàn)了數(shù)學(xué)的對(duì)稱美．如圖，將一個(gè)正方體沿交于一頂點(diǎn)的三條棱的中點(diǎn)截去一個(gè)三棱錐，共可截去八個(gè)三棱錐，得到八個(gè)面為正三角形，六個(gè)面為正方形的“阿基米德多面體”，則該多面體中具有公共頂點(diǎn)的兩個(gè)正三角形所在平面的夾角正切值為（ ）發(fā)布：2024/11/9 21:30:1組卷：174引用：3難度：0.5 -
2．如圖，三棱柱ABC-A1B1C1滿足棱長都相等且AA1⊥平面ABC，D是棱CC1的中點(diǎn)，E是棱AA1上的動(dòng)點(diǎn)．設(shè)AE=x,隨著x增大，平面BDE與底面ABC所成銳二面角的平面角是（ ）發(fā)布：2024/12/11 21:0:1組卷：1640引用：12難度：0.3 -
3．如圖，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=2，BC=CC1=4，點(diǎn)D是棱AB的中點(diǎn)，則平面ABB1A1與平面B1CD所成角的正弦值為（ ）發(fā)布：2024/11/15 14:30:2組卷：449引用：2難度：0.6