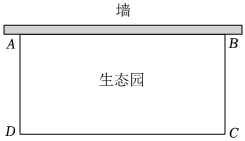
如圖，為了便于勞動(dòng)課程的開展，學(xué)校打算建一個(gè)矩形生態(tài)園ABCD（如圖），生態(tài)園一面靠墻（墻長30m），另外三面用80m的籬笆圍成．設(shè)矩形ABCD的邊AB=x m,面積為S m2．
（1）寫出S與x之間的函數(shù)表達(dá)式，并寫出x的取值范圍；
（2）當(dāng)AB為多少米時(shí)，生態(tài)園的面積最大？最大值是多少？
【考點(diǎn)】二次函數(shù)的應(yīng)用．
【答案】（1）S=-x2+40x，0＜x≤30；
（2）當(dāng)AB為30米時(shí)，生態(tài)園的面積最大，最大值為750平方米．
1
2
（2）當(dāng)AB為30米時(shí)，生態(tài)園的面積最大，最大值為750平方米．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/28 16:0:2組卷：62引用：2難度：0.6
相似題
-
1．如圖，灌溉車為綠化帶澆水，噴水口H離地豎直高度OH為1.2m.可以把灌溉車噴出水的上、下邊緣抽象為平面直角坐標(biāo)系中兩條拋物線的部分圖象；把綠化帶橫截面抽象為矩形DEFG，其水平寬度DE=3m,豎直高度EF=0.5m.下邊緣拋物線是由上邊緣拋物線向左平移得到，上邊拋物線最高點(diǎn)A離噴水口的水平距離為2m,高出噴水口0.4m,灌溉車到綠化帶的距離OD為d（單位：m）．
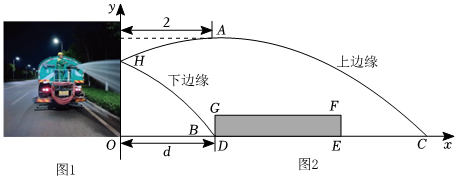
（1）求上邊緣拋物線的函數(shù)解析式；
（2）求下邊緣拋物線與x軸的正半軸交點(diǎn)B的坐標(biāo)；
（3）要使灌溉車行駛時(shí)噴出的水能澆灌到整個(gè)綠化帶，求出d的取值范圍．發(fā)布：2025/5/24 7:30:1組卷：427引用：1難度：0.3 -
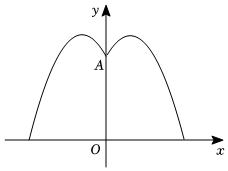2．某公園要修建一個(gè)圓形噴水池，在池中心豎直安裝一根水管，水管OA長2.25m.在水管的頂端安裝一個(gè)噴水頭，使噴出的拋物線形水柱在與池中心的水平距離為1m處達(dá)到最高，高度為3m.
（1）建立如圖所示平面直角坐標(biāo)系，求拋物線（第一象限部分）的解析式；
（2）不考慮其它因素，水池的直徑至少要多少米才能使噴出的水流不落到池外？
（3）實(shí)際施工時(shí)，經(jīng)測量，水池的最大半徑只有2.5m,在不改變噴出的拋物線形水柱形狀的情況下，且噴出的拋物線形水柱在與池中心的水平距離為1m處達(dá)到最高，需對(duì)水管的長度進(jìn)行調(diào)整，求調(diào)整后水管的最大長度．發(fā)布：2025/5/24 7:30:1組卷：1730引用：5難度：0.6 -
3．兔年來臨之際，某商店銷售一種小兔子毛絨玩具，每件進(jìn)價(jià)為30元，經(jīng)過試銷發(fā)現(xiàn)，該玩具每天的銷售量y（件）與銷售單價(jià)x（元）之間滿足如下關(guān)系：y=-x+60．
（1）求該商店銷售這種毛絨玩具每天獲得的利潤w（元）與x之間的函數(shù)關(guān)系式；
（2）若商店銷售這種毛絨玩具每天想獲得200元的利潤，且最大限度讓利給顧客，則銷售單價(jià)應(yīng)定為多少元？發(fā)布：2025/5/24 7:0:1組卷：84引用：1難度：0.6