綜合與實踐
旋轉是初中學習的一種全等變換，通過旋轉可以將已知條件中“分散”的條件相對地“集中”在一起，構成新的聯系，從而解決問題．同時，旋轉時圖形中出現“有公共端點的線段相等”的條件，所以在等腰（或等邊）三角形、正方形中常進行旋轉變換．
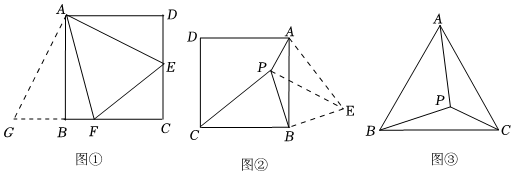
（1）正方形中的“旋轉”：如圖①，點E、點F分別是正方形的邊DC、BC上的點，連接AF、FE、AE，若∠EAF=45°，則BF、DE、EF之間的數量關系為 BF+DE=EFBF+DE=EF．
問題解決：將△ADE繞點A順時針旋轉90°，得到△ABG，則點G點B、點F三點 共線共線，可證明△AEF≌△AGF△AGF，從而得出結論，請你完成上述全等關系的證明．
（2）如圖②，P為正方形ABCD內一點，且PA=1，PB=2，PC=3，請你確定∠APB的度數：∠APB=135°135°．
小杰同學的思路是：設法將PA、PB、PC相對集中，于是將△BCP繞點B順時針旋轉90．得到△BAE，連接PE，確定ΔΡBE與△APE的形狀分別為：等腰直角三角形和直角三角形等腰直角三角形和直角三角形，問題得以解決．
（3）等邊三角形中的“旋轉”：請你參考小杰同學的思路，解決下面問題：
如圖③，P點是等邊三角形ABC內一點，若∠APB=115°，∠APC=120°，請你直接寫出：以線段PA、PB、PC的長度為邊長的三角形的各內角的度數分別為 60°，65°和55°60°，65°和55°．
【考點】四邊形綜合題．
【答案】BF+DE=EF；共線；△AGF；135°；等腰直角三角形和直角三角形；60°，65°和55°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：368引用：2難度：0.1
相似題
-
1．在平行四邊形ABCD中，M，N分別是邊AD，AB的點，AB=kAN，AD=kAM．
（1）如圖1，若連接MN，BD，求證：MN∥BD；
（2）如圖2，把△AMN繞點A順時針旋轉角度α（0°＜α＜90°）得到△AFE，M，N的對應點分別為點E，F，連接BE，若∠ABF=∠EBC，∠AEB=2∠DAE．
①直接寫出k的取值范圍；
②當tan∠EBC=時，求k的值．13
發布：2025/5/26 11:30:1組卷：207引用：3難度：0.2 -
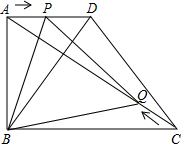2．如圖，在四邊形ABCD中，AD∥BC，∠DAB=90°，AB=6cm,BC=8cm,AD=4cm.點P從點A出發沿AD向點D勻速運動，速度是1cm/s；同時，點Q從點C出發沿CA 向點A勻速運動，速度是1cm/s,當一個點到達終點，另一個點立即停止運動．連接PQ，BP，BQ，設運動時間為t（s），解答下列問題：
（1）當t為何值時，PQ∥CD？
（2）設△BPQ的面積為s（cm2），求s與t之間的函數關系式；
（3）是否存在某一時刻t,使得△BPQ的面積為四邊形ABCD面積的？若存在，求出此時t的值；若不存在，說明理由；12
（4）連接BD，是否存在某一時刻t,使得BP平分∠ABD？若存在，求出此時t的值；若不存在，說明理由．發布：2025/5/26 12:0:1組卷：399引用：2難度：0.1 -
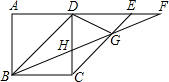3．如圖，正方形ABCD中，在AD的延長線上取點E，F，使DE=AD，DF=BD，連接BF分別交CD，CE于H，G下列結論正確的有．（填序號）
①GD=GH；②EC=2DG；③S△CDG=S四邊形DHGE； ④圖中有7個等腰三角形．發布：2025/5/27 4:0:1組卷：172引用：1難度：0.5