2022年黑龍江省齊齊哈爾市建華區中考數學二模試卷

一、選擇題（每小題3分，滿分30分）

• 1．-4的相反數是（　　）

  A．4

  B．-4

  C．-0.25

  D．0.25
  組卷：169引用：1難度：0.9

  解析

• 2．欣賞圖形的對稱之美：如圖安全標志圖片中，是軸對稱圖形的是（　　）

  A． 有機產品	B． 農業部948蘋果項目
  C． 節水產品認證	D． 綠色食品
  組卷：51引用：1難度：0.9

  解析

• 3．某課外興趣小組為了解所在地區老年人的健康狀況，分別作了四種不同的抽樣調查．你認為抽樣比較合理的是（　　）

  A．在公園調查了1000名老年人的健康狀況

  B．在醫院調查了1000名老年人的健康狀況

  C．調查了10名老年鄰居的健康狀況

  D．利用派出所的戶籍網隨機調查了該地區10%的老年人的健康狀況
  組卷：728引用：56難度：0.9

  解析

• 4．已知點P（a-2，4-a）關于原點對稱的點在第三象限，則a的取值范圍在數軸上表示正確的是（　　）

  A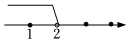．	B．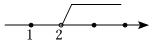
  C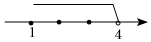．	D．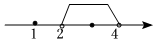
  組卷：136引用：3難度：0.7

  解析

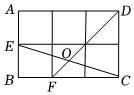• 5．如圖，矩形ABCD由6個邊長為1的小正方形組成，連接小正方形的頂點E、C及D、F交于點O，則tan∠DOC的值為（　　）

  A． 5

  B．2

  C． 3

  D． 2
  組卷：56引用：1難度：0.5

  解析

• 6．若關于x的分式方程

  ax

  x

  -

  1

  =

  3

  a

  +

  2

  x

  -

  1

  +

  1

  無解，則a的值為（　　）

  A．-1

  B．1

  C．1或2

  D．-1或1
  組卷：246引用：1難度：0.6

  解析

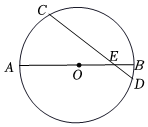• 7．如圖，⊙O的直徑AB與弦CD相交于點E，若AE=5，EB=1，∠AEC=30°，則CD的長為（　　）

  A．5

  B．2 3

  C．4 2

  D． 2 2 + 3 + 1
  組卷：1816引用：2難度：0.6

  解析

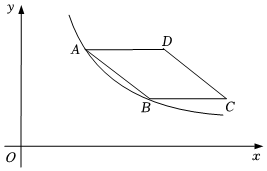• 8．如圖，菱形ABCD的邊AD與x軸平行，A、B兩點的橫坐標分別為4、8，若反比例函數y=

  24

  x

  的圖象經過A、B兩點，則菱形ABCD的面積為（　　）

  A．12

  B．15

  C．24

  D．30
  組卷：211引用：2難度：0.6

  解析

三、解答題（本題共7道大題，共69分）

• 23．綜合與實踐
  旋轉是初中學習的一種全等變換，通過旋轉可以將已知條件中“分散”的條件相對地“集中”在一起，構成新的聯系，從而解決問題．同時，旋轉時圖形中出現“有公共端點的線段相等”的條件，所以在等腰（或等邊）三角形、正方形中常進行旋轉變換．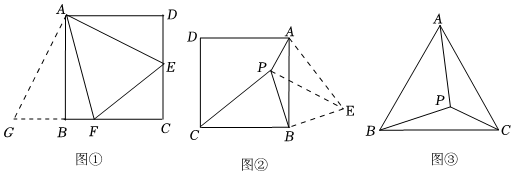
  
  （1）正方形中的“旋轉”：如圖①，點E、點F分別是正方形的邊DC、BC上的點，連接AF、FE、AE，若∠EAF=45°，則BF、DE、EF之間的數量關系為

  ．
  問題解決：將△ADE繞點A順時針旋轉90°，得到△ABG，則點G點B、點F三點

  ，可證明△AEF≌

  ，從而得出結論，請你完成上述全等關系的證明．
  （2）如圖②，P為正方形ABCD內一點，且PA=1，PB=2，PC=3，請你確定∠APB的度數：∠APB=

  ．
  小杰同學的思路是：設法將PA、PB、PC相對集中，于是將△BCP繞點B順時針旋轉90．得到△BAE，連接PE，確定ΔΡBE與△APE的形狀分別為：

  ，問題得以解決．
  （3）等邊三角形中的“旋轉”：請你參考小杰同學的思路，解決下面問題：
  如圖③，P點是等邊三角形ABC內一點，若∠APB=115°，∠APC=120°，請你直接寫出：以線段PA、PB、PC的長度為邊長的三角形的各內角的度數分別為

  ．
  組卷：368引用：2難度：0.1

  解析

• 24．綜合與實踐
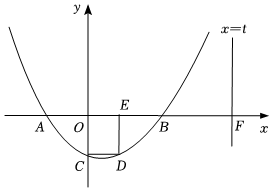
  如圖，已知正方形OCDE中，頂點E（1，0），拋物線y=

  1

  2

  x²+bx+c經過點C、點D，與x軸交于A、B兩點（點B在點A的右側），直線x=t（t＞0）交x軸于點F．
  （1）求拋物線的解析式，且直接寫出點A、點B的坐標；
  （2）若點G是拋物線的對稱軸上一動點，且使AG+CG最小，則G點坐標為：

  ；
  （3）在直線x=t（第一象限部分）上找一點P，使得以點P、點B、點F為頂點的三角形與△OBC全等，請你直接寫出點P的坐標；
  （4）點M是射線AC上一點，點N為平面上一點，是否存在這樣的點M，使得以點O、點A、點M、點N為頂點的四邊形為菱形？若存在，請你直接寫出點N的坐標；若不存在，請說明理由．
  組卷：304引用：1難度：0.3

  解析