CD是經過∠BCA頂點C的一條直線，CA=CB．E，F分別是直線CD上兩點，且∠BEC=∠CFA=∠α．
（1）若直線CD經過∠BCA的內部，且E，F在射線CD上．
①如圖1，若∠BCA=90°，∠α=90°，則BE==CF；
②如圖2，若0°＜∠BCA＜180°，請添加一個關于∠α與∠BCA關系的條件∠α+∠ACB=180°∠α+∠ACB=180°，使①中的結論仍然成立，并說明理由．
（2）如圖3，若直線CD經過∠BCA的外部，∠α=∠BCA，請提出EF，BE，AF三條線段間數量關系的合理猜想：EF=BE+AFEF=BE+AF．
【考點】三角形綜合題．
【答案】=；∠α+∠ACB=180°；EF=BE+AF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：525引用：10難度：0.3
相似題
-
1．先閱讀下面一段文字，再回答問題：
已知在平面直角坐標系xOy中，對于任意兩點P1（x1，y1）與P2（x2，y2）的“識別距離”，給出如下定義：若|x1-x2|＞|y1-y2|，則點P1（x1，y1）與P2（x2，y2）的“識別距離”為|x1-x2|；若|x1-x2|＜|y1-y2|，則點P1（x1，y1）與P2（x2，y2）的“識別距離”為|y1-y2|；
（1）已知點A（-1，0），B為y軸上的動點．
①若點A與點B的“識別距離”為3，寫出滿足條件的點B的坐標；
②直接寫出點A與點B的“識別距離”的最小值．
（2）已知點，D（1，1），求點C與點D的“識別距離”的最小值及相應的點C的坐標．C（m,34m+3）發布：2025/6/6 1:30:1組卷：241引用：1難度：0.1 -
2．將兩塊直角三角板（即兩個直角三角形，其中∠C=30°，∠CDO=60°；∠OAB=∠OBA=45°） 的直角頂點O按圖1方式疊放在一起，△COD繞著點O順時針旋轉一周，旋轉的速度為每秒10°，若旋轉時間為t秒，請回答下列問題：
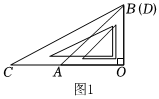
（1）當t=9時，直線OD與OB的位置關系是 ；當0＜t＜9時，（如圖2及其簡化圖），∠BOC的度數為 （用含t的代數式表示）．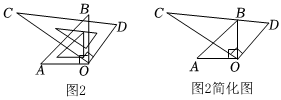
（2）當邊OB∥CD時，t的值是 ．
（3）當邊AB∥CD時，求t的值．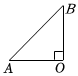
發布：2025/6/6 1:30:1組卷：109引用：1難度：0.2 -
3．把兩個等腰直角△ABC和△ADE按如圖1所示的位置擺放，∠A=90°，將△ADE繞點A按逆時針方向旋轉，如圖2，連接BD，EC，設旋轉角為α（0°＜α＜360°）．
（1）求證：△BAD≌△CAE；
（2）如圖3，若點D在線段BE上，且BC=13，DE=7，求CE的長；
（3）當△ABD的面積最大時，請直接寫出此時旋轉角α的度數．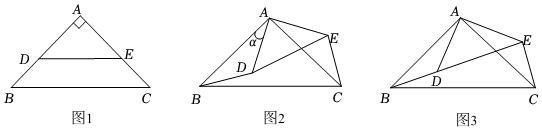
發布：2025/6/6 2:0:9組卷：460引用：3難度：0.1