已知x=a2-ab,y=ab-b2，x與y的大小關系是（ ）
【考點】配方法的應用；非負數的性質：偶次方．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/19 17:0:4組卷：133引用：1難度：0.8
相似題
-
1．（1）已知3m=6，3n=2，求32m+n-1的值；
（2）已知a2+b2+2a-4b+5=0，求（a-b）-3的值．發布：2025/6/7 10:30:1組卷：194引用：3難度：0.5 -
2．在學了乘法公式“（a±b）2=a2±2ab+b2”的應用后，王老師提出問題：求代數式x2+4x+5的最小值．要求同學們運用所學知識進行解答．
同學們經過探索、交流和討論，最后總結出如下解答方法；
解：x2+4x+5=x2+4x+22-22+5=（x+2）2+1，
∵（x+2）2≥0，∴（x+2）2+1≥1．
當（x+2）2=0時，（x+2）2+1的值最小，最小值是1．
∴x2+4x+5的最小值是1．
請你根據上述方法，解答下列各題：
（1）直接寫出（x-1）2+3的最小值為 ．
（2）求代數式x2+10x+32的最小值．
（3）你認為代數式-+2x+5有最大值還是有最小值？求出該最大值或最小值．13x2
（4）若7x-x2+y-11=0，求x+y的最小值．發布：2025/6/7 11:0:1組卷：1135引用：4難度：0.5 -
3．閱讀下列材料：
利用完全平方公式，將多項式x2+bx+c變形為（x+m）2+n的形式，然后由（x+m）2≥0就可求出多項式x2+bx+c的最小值．
例題：求x2-12x+37的最小值：
解：x2-12x+37=x2-2x?6+62-62+37=（x-6）2+1
因為不論x取何值，（x-6）2總是非負數，即（x-6）2≥0．
所以（x-6）2+1≥1．
所以當x=6時，x2-12x+37有最小值，最小值是1．
根據上述材料，解答下列問題：
（1）填空：x2-8x+=（x-）2；
（2）將x2+10x-2變形為（x+m）2+n的形式，并求出x2+10x-2的最小值；
（3）如圖所示的第一個長方形邊長分別是2a+5、3a+2，面積為S1；如圖所示的第二個長方形邊長分別是5a、a+5，面積為S2；試比較S1與S2的大小，并說明理由．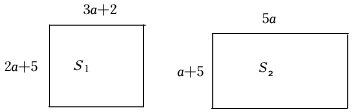
發布：2025/6/7 8:30:2組卷：174引用：1難度：0.4