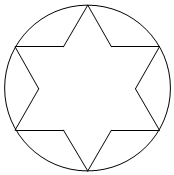
1904年，瑞典數學家柯克構造了一種曲線，取一個正三角形，在每個邊以中間的13部分為一邊，向外凸出作一個正三角形，再把原來邊上中間的13部分擦掉，就成了一個很像雪花的六角星，如圖所示．現在向圓中均勻的散落1000粒豆子，則落在六角星中的豆子數約為（ ）（π≈3，3≈1.732）
1
3
1
3
3
【考點】幾何概型．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 14:0:0組卷：81引用：5難度：0.7
相似題
-
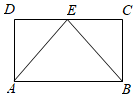1．如圖，矩形ABCD中，點E為邊CD的中點，若在矩形ABCD內部隨機取一個點Q，則點Q取自△ABE內部的概率等于．發布：2025/1/13 8:0:2組卷：30引用：12難度：0.7 -
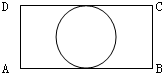2．如圖所示，在矩形ABCD中，AB=4cm,BC=2cm,在圖形上隨機撒一粒黃豆，則黃豆落到圓上的概率是．發布：2025/1/13 8:0:2組卷：9引用：2難度：0.7 -
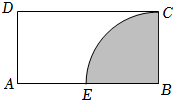3．如圖，矩形ABCD，AB=2，BC=1，陰影部分為B為圓心，BC為半徑的圓與矩形的重合部分，現在向矩形內隨機投擲一點，則該點落在陰影部分以外的概率為（ ）發布：2024/12/29 15:30:4組卷：1引用：1難度：0.7