當前位置：試卷中心 > 試卷詳情

2023年河南省五市高考數學第二次聯考試卷（文科）

發布：2025/1/1 21:30:3

一、選擇題：本題共12個小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知集合A={y|y=x²}，B={x|y=ln（2-x）}，則A∪B=（　　）
A．R B．（0，2） C．[0，2） D．（0，+∞）
組卷：39引用：2難度：0.7
解析
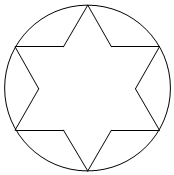2．1904年，瑞典數學家柯克構造了一種曲線，取一個正三角形，在每個邊以中間的
1
3
部分為一邊，向外凸出作一個正三角形，再把原來邊上中間的
1
3
部分擦掉，就成了一個很像雪花的六角星，如圖所示．現在向圓中均勻的散落1000粒豆子，則落在六角星中的豆子數約為（　　）（π≈3，
3
≈1.732）
A．577 B．508 C．481 D．331
組卷：81引用：5難度：0.7
解析
3．要計算
S
=
1
+
1
2
+
1
3
+
…
+
1
2023
的結果，如圖程序框圖中的判斷框內可以填（　　）
A．n＜2023 B．n≤2023 C．n＞2023 D．n≥2023
組卷：20引用：3難度：0.8
解析
4．已知
α
-
β
=
π
6
，tanα-tanβ=3，則cos（α+β）的值為（　　）
A．
1
2
+
3
3
B．
1
2
-
3
3
C．
1
3
+
3
2
D．
1
3
-
3
2
組卷：370引用：10難度：0.8
解析
5．已知等差數列{a_n}的公差為d,前n項和為S_n，則“d＞0”是“S_3n-S_2n＞S_2n-S_n”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：413引用：8難度：0.6
解析
6．美國生物學家和人口統計學家雷蒙德?皮爾提出一種能較好地描述生物生長規律的生長曲線，稱為“皮爾曲線”，常用的“皮爾曲線”的函數解析式可以簡化為
f
（
x
）
=
P
1
+
a
kx
+
b
（
P
＞
0
，
a
＞
1
，
k
＜
0
）
的形式．已知
f
（
x
）
=
6
1
+
3
kx
+
b
（
x
∈
N
）
描述的是一種果樹的高度隨著栽種時間x（單位：年）變化的規律，若剛栽種（x=0）時該果樹的高為1.5m,經過2年，該果樹的高為4.5m,則該果樹的高度不低于5.4m,至少需要（　　）
A．3年 B．4年 C．5年 D．6年
組卷：127引用：8難度：0.6
解析
7．函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
+
b
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖象如圖所示，現將y=f（x）的圖象上所有點的橫坐標伸長到原來的2倍（縱坐標不變），再向下平移1個單位所得圖象對應的函數為g（x），則下列結論正確的是（　　）
A．函數f（x）在區間
[
π
6
，
5
π
6
]
單調遞減
B．
g
（
-
π
12
）
=
2
C．點
（
π
6
，
0
）
是函數g（x）圖象的一個對稱中心
D．直線
x
=
π
6
是函數y=f（x）的一條對稱軸
組卷：136引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

（二）選考題：共10分，請考生從第22，23兩題中任選一題作答．如果多做，則按所做的第一個題目計分．選修4-4：坐標系與參數方程

22．在直角坐標系xOy中，曲線C的參數方程為
x
=
1
+
cosα
y
=
1
+
sinα
（α為參數）．以坐標原點為極點，x軸的非負半軸為極軸建立極坐標系，直線l的極坐標方程為
ρsinθ
-
3
ρcosθ
+
1
=
0
．
（1）求曲線C的普通方程和直線l的直角坐標方程；
（2）若點P（0，-1），直線l與曲線C的交點為M，N，求|PM|+|PN|的值．
組卷：100引用：7難度：0.5
解析