當(dāng)前位置：
2022-2023學(xué)年四川省達(dá)州市達(dá)川區(qū)萬(wàn)家初級(jí)中學(xué)八年級(jí)（上）期末數(shù)學(xué)試卷>
試題詳情
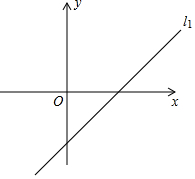表格中的兩組對(duì)應(yīng)值滿(mǎn)足一次函數(shù)y=kx+b,函數(shù)圖象為直線(xiàn)l1，如圖所示．將函數(shù)y=kx+b中的k與b交換位置后得一次函數(shù)y=bx+k,其圖象為直線(xiàn)l2.設(shè)直線(xiàn)l1交y軸于點(diǎn)A，直線(xiàn)l1交直線(xiàn)l2于點(diǎn)B，直線(xiàn)l2交y軸于點(diǎn)C．
| x | -2 | 4 |
| y | -4 | 2 |
（2）若點(diǎn)P在直線(xiàn)l1上，且△BCP的面積是△ABC的面積的（1+?
2
（3）若直線(xiàn)y=a分別與直線(xiàn)l1，l2及y軸的三個(gè)交點(diǎn)中，其中一點(diǎn)是另兩點(diǎn)所成線(xiàn)段的中點(diǎn)，求a的值．
【考點(diǎn)】一次函數(shù)綜合題．
【答案】（1）y=-2x+1．
（2）P的坐標(biāo)為（-，-2-）或（2+，）；
（3）a的值為-5或-或-．
（2）P的坐標(biāo)為（-
2
2
2
2
（3）a的值為-5或-
7
5
1
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/7 4:0:8組卷：576引用：2難度：0.3
相似題
-
1．在平面直角坐標(biāo)系xOy中，已知點(diǎn)M（m,n），我們將點(diǎn)M的橫縱坐標(biāo)交換位置得到點(diǎn)N（n,m）．給出如下定義：對(duì)于平面上的點(diǎn)C，若滿(mǎn)足NC=1，則稱(chēng)點(diǎn)C為點(diǎn)M的“對(duì)炫點(diǎn)”．
（1）已知點(diǎn)A（2，0），
①下列各點(diǎn)：Q1（0，1），Q2（1，1），Q3（-1，2）中為點(diǎn)A的“對(duì)炫點(diǎn)”的是 ；
②點(diǎn)P是直線(xiàn)y=x+2上一點(diǎn)，若點(diǎn)A是點(diǎn)P的對(duì)炫點(diǎn)，求出點(diǎn)P的坐標(biāo)；
（2）設(shè)點(diǎn)A（a,b）是第一象限內(nèi)一點(diǎn)，點(diǎn)P是直線(xiàn)y=x+b上一點(diǎn)，至少存在一個(gè)點(diǎn)P，使得點(diǎn)A的對(duì)炫點(diǎn)也是點(diǎn)P的對(duì)炫點(diǎn)，求a、b的取值范圍．發(fā)布：2025/5/22 5:30:2組卷：622引用：1難度：0.3 -
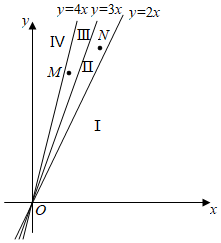2．等腰三角形ABC中，AB=AC，記AB=x,周長(zhǎng)為y,定義（x,y）為這個(gè)三角形的坐標(biāo)．如圖所示，直線(xiàn)y=2x,y=3x,y=4x將第一象限劃分為4個(gè)區(qū)域．下面四個(gè)結(jié)論中，
①對(duì)于任意等腰三角形ABC，其坐標(biāo)不可能位于區(qū)域Ⅰ中；
②對(duì)于任意等腰三角形ABC，其坐標(biāo)可能位于區(qū)域Ⅳ中；
③若三角形ABC是等腰直角三角形，其坐標(biāo)位于區(qū)域Ⅲ中；
④圖中點(diǎn)M所對(duì)應(yīng)等腰三角形的底邊比點(diǎn)N所對(duì)應(yīng)等腰三角形的底邊長(zhǎng)．
所有正確結(jié)論的序號(hào)是（ ）發(fā)布：2025/5/22 10:0:1組卷：1665引用：10難度：0.2 -
3．如圖，在平面直角坐標(biāo)系中，點(diǎn)O為坐標(biāo)原點(diǎn)，直線(xiàn)y=-x+7分別交x、y軸于A、B兩點(diǎn)，直線(xiàn)y=k1x+15分別交x軸、y軸于C、D兩點(diǎn)，BD：AC=8：3．
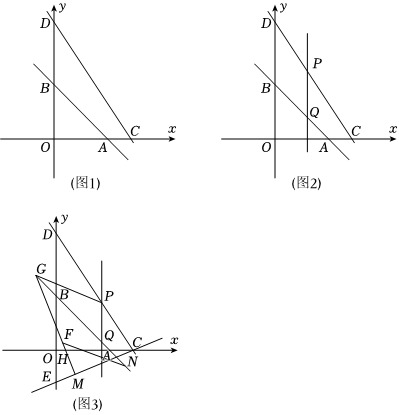
（1）如圖1，求k1的值；
（2）如圖2，點(diǎn)Q為線(xiàn)段AB上一動(dòng)點(diǎn)，過(guò)點(diǎn)Q作PQ⊥x軸，交線(xiàn)段CD于點(diǎn)P，設(shè)點(diǎn)Q的橫坐標(biāo)為t,線(xiàn)段PQ的長(zhǎng)度為d,求d與t之間的函數(shù)解析式（不要求寫(xiě)出自變量t的取值范圍）；
（3）如圖3，在（2）的條件下，過(guò)點(diǎn)C的直線(xiàn)y=k2x-4交y軸于點(diǎn)E，點(diǎn)P關(guān)于直線(xiàn)AB的對(duì)稱(chēng)點(diǎn)為點(diǎn)F，G為線(xiàn)段AB延長(zhǎng)線(xiàn)上一點(diǎn)，，連接GF并延長(zhǎng)交x軸于點(diǎn)H，交線(xiàn)段CE于點(diǎn)M，N為線(xiàn)段BA延長(zhǎng)線(xiàn)上一點(diǎn)，連接FN，F(xiàn)N=2MF，∠MHC-∠BNF=45°，求點(diǎn)N的坐標(biāo)．BG=22
?
發(fā)布：2025/5/21 21:0:1組卷：249引用：1難度：0.1