問題提出：
我們知道，過任意一個三角形的三個頂點能作一個圓，過任意一個四邊形的四個頂點能作一個圓嗎？
初步思考：
（1）給出了一些特殊的四邊形：①矩形②菱形③等腰梯形④正方形，能過它們四個頂點作一個圓的是 ①③④①③④（填寫序號），過某個四邊形四個頂點作一個圓的四邊形相對的兩個內角的關系是 互補（對角之和等于180°）互補（對角之和等于180°）．
進一步研究：
（2）如果過某個四邊形的四個頂點不能作一個圓，那么其相對的兩個內角之間有上面的關系嗎？請結合圖1的兩幅圖說明其中的道理．（提示：考慮∠B+∠D與180°之間的關系）
由上面的探究，請用文字語言直接寫出過某個四邊形的四個頂點能作一個圓的條件 對角互補對角互補．
拓展延伸
（3）如何過圓上一點，僅用沒有刻度的直尺，作出已知直徑的垂線？
已知：如圖2，AB是⊙O的直徑，點C在⊙O上，求作：CN⊥AB．
作法：①連接CA，CB；
②在?CB上任取異于B、C的一點D，連接DA，DB；
③DA與CB相交于E點，延長AC、BD，交于F點；
④連接F、E并延長，交直徑AB于M：
⑤連接D、M并延長，交⊙O于N．連接CN．
則CN⊥AB．
請按上述作法在圖2中作圖，并說明CN⊥AB的理由，（提示：可以利用（2）中的結論）
?
CB
【考點】圓的綜合題．
【答案】①③④；互補（對角之和等于180°）；對角互補
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：257引用：1難度：0.2
相似題
-
1．若AC=4，以點C為圓心，2為半徑作圓，點P為該圓上的動點，連接AP．
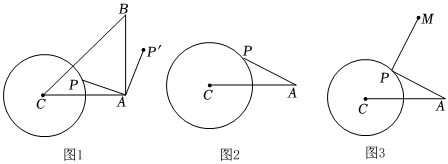
（1）如圖1，取點B，使△ABC為等腰直角三角形，∠BAC=90°，將點P繞點A順時針旋轉90°得到AP′．
①點P'的軌跡是 （填“線段”或者“圓”）；
②CP'的最小值是 ；
（2）如圖2，以AP為邊作等邊△APQ（點A、P、Q按照順時針方向排列），在點P運動過程中，求CQ的最大值．
（3）如圖3，將點A繞點P逆時針旋轉90°，得到點M，連接PM，則CM的最小值為 ．發布：2025/5/24 11:30:1組卷：521引用：2難度：0.3 -
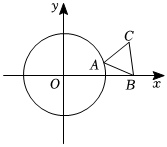2．如圖，⊙O的半徑為，正三角形ABC的頂點B的坐標為（2，0），頂點A在⊙O上運動．3
（1）當點A在x軸正半軸上時，求點C的坐標；
（2）點A在運動過程中，是否存在直線AB與⊙O相切的位置關系？若存在，請直接寫出點C的坐標；
（3）設點A的橫坐標為x,△ABC的面積為S，求S與x之間的函數關系式，并求出S的最大值與最小值．發布：2025/5/24 10:30:2組卷：77引用：4難度：0.4 -
3．如圖1，CD是⊙O的弦，半徑OA⊥CD，垂足為B，過點C作⊙O的切線l.
（1）若點E在⊙O上，且=?CE，連接OE．?CA
①連接AE，求證：AE∥l；
②如圖2，若B是OA的中點，連接OD，求證：DE是⊙O的直徑；
（2）如圖3，過點B作BF⊥l,垂足為F，若⊙O的半徑是4，求BC-BF的最大值．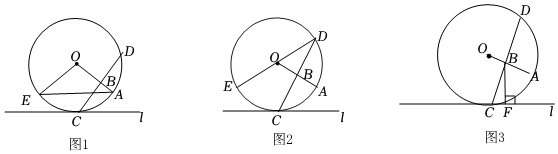
發布：2025/5/24 11:0:1組卷：345引用：3難度：0.3