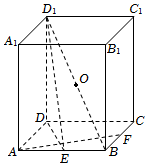
如圖，在正四棱柱ABCD-A₁B₁C₁D₁中，E為AB的中點，F為BC的中點，O為BD₁的中點．
（1）求證：AF⊥平面DD₁E；
（2）線段AF上是否存在點G，使得OG∥平面DD₁E，若存在，求出
AG
GF
的值，若不存在，請說明理由．

【答案】（1）證明過程見解析，（2）

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：248引用：3難度：0.6

相似題

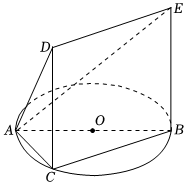1．?如圖，一簡單組合體的一個面ABC內接于圓O，AB是圓O的直徑，四邊形DCBE為平行四邊形，且DC⊥平面ABC．
（1）證明：BC⊥平面ACD；
（2）若AB=2，BC=1，tan∠EAB=
3
2
，試求該簡單組合體的體積V．
發布：2025/1/20 8:0:1組卷：25引用：1難度：0.5
解析
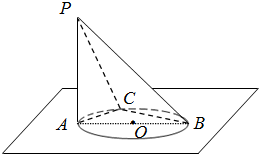2．如圖，AB是圓O的直徑，PA垂直于圓O所在的平面，C是圓周上不同于A、B的任意一點．
（1）求證：BC⊥平面PAC；
（2）求證：平面PAC⊥平面PBC．
發布：2025/1/28 8:0:2組卷：124引用：3難度：0.3
解析
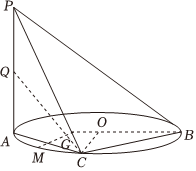3．如圖，AB是圓O的直徑，PA垂直于圓O所在的平面，C是圓O上異于A，B的點，
（1）求證：BC⊥平面PAC；
（2）設Q，M分別為PA，AC的中點，問：對于線段OM上的任一點G，是否都有QG∥平面PBC？并說明理由．
發布：2025/1/28 8:0:2組卷：34引用：2難度：0.3
解析

相關試卷

如圖，在正四棱柱ABCD-A1B1C1D1中，E為AB的中點，F為BC的中點，O為BD1的中點．（1）求證：AF⊥平面DD1E；（2）線段AF上是否存在點G，使得OG∥平面DD1E，若存在，求出AGGF的值，若不存在，請說明理由．