定義：我們知道，四邊形的一條對角線把這個四邊形分成了兩個三角形，如果這兩個三角形相似（不全等），我們就把這條對角線叫做這個四邊形的“相似對角線”．
理解：（1）如圖1，若四邊形ABCD是以AC為“相似對角線”的四邊形，AB=1，BC=2，
∠ABC=∠ACD=90°，求出CD的長度．
（2）如圖2，在四邊形ABCD中，∠ABC=70°，∠ADC=145°，對角線BD平分∠ABC．請問BD是四邊形ABCD的“相似對角線”嗎？請說明理由；
（3）運用：
如圖3，已知FH是四邊形EFGH的“相似對角線”，∠EFH=∠HFG=30°．連接EG，若△EFG的面積為83，求FH的長
8
3
【考點】相似形綜合題．
【答案】（1）2 或；
（2）BD是四邊形ABCD的“相似對角線”，理由見解析；
（3）4．
5
5
2
（2）BD是四邊形ABCD的“相似對角線”，理由見解析；
（3）4
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：191引用：1難度：0.3
相似題
-
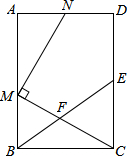1．如圖，在矩形ABCD中，E為CD的中點，F為BE上的一點，連接CF并延長交AB于點M，MN⊥CM交射線AD于點N．
（1）當F為BE中點時，求證：AM=CE；
（2）若=ABBC=2，求EFBF的值；ANND
（3）若=ABBC=n,當n為何值時，MN∥BE？EFBF發布：2025/5/27 2:30:1組卷：1756引用：15難度：0.1 -
2．如圖，平面直角坐標系中，四邊形OABC為矩形，點A、B的坐標為（6，0），（6，8）．動點M、N分別從O、B同時出發，都以每秒1個單位的速度運動，其中，點M沿OA向終點A運動，點N沿BC向終點C運動，過點N作NP⊥BC，交AC于點P，連接MP，已知動點運動了x秒．
（1）用含x的代數式表示P的坐標（直接寫出答案）；
（2）設y=S四邊形OMPC，求y的最小值，并求此時x的值；
（3）是否存在x的值，使以P、A、M為頂點的三角形與△AOC相似？若存在，請求出x的值；若不存在，請說明理由．發布：2025/5/26 8:30:1組卷：432引用：3難度：0.7 -
3．綜合與實踐
【問題情境】
在綜合與實踐課上，同學們以“A4紙片的折疊”為主題開展數學活動．如圖①，在矩形A4紙片ABCD中，AB長為21cm,AD長為30cm.
【操作發現】
第一步：如圖②，將矩形紙片ABCD對折，使AB與DC重合，得到折痕EF，再將紙片展平，則AE=cm.
第二步：如圖③，將矩形紙片ABCD沿BE折疊，使點A的對應點M落在矩形ABCD的內部，再將紙片沿過點E的直線折疊，使ED與EM重合，折痕為EN，則∠BEN=度．
【結論應用】
在圖③中，運用以上操作所得結論，解答下列問題：
（1）求證：△BME∽△EMN．
（2）直接寫出線段CN的長為 cm.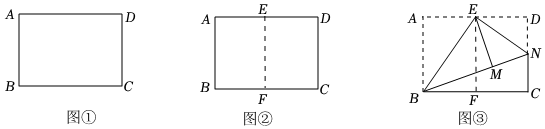
發布：2025/5/26 9:30:1組卷：397引用：4難度：0.3