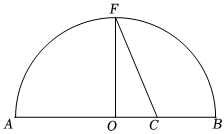
 《幾何原本》卷Ⅱ的幾何代數(shù)法成了后世西方數(shù)學(xué)家處理數(shù)學(xué)問題的重要依據(jù).通過這一原理,很多代數(shù)的定理都能夠通過圓形實(shí)現(xiàn)證明,也稱之為無字證明現(xiàn)有如圖所示圖形,點(diǎn)F在半圓O上,點(diǎn)C在直徑AB上,且OF⊥AB,設(shè)AC=a,BC=b,可以直接通過比較線段OF與線段CF的長(zhǎng)度完成的無字證明為( )
《幾何原本》卷Ⅱ的幾何代數(shù)法成了后世西方數(shù)學(xué)家處理數(shù)學(xué)問題的重要依據(jù).通過這一原理,很多代數(shù)的定理都能夠通過圓形實(shí)現(xiàn)證明,也稱之為無字證明現(xiàn)有如圖所示圖形,點(diǎn)F在半圓O上,點(diǎn)C在直徑AB上,且OF⊥AB,設(shè)AC=a,BC=b,可以直接通過比較線段OF與線段CF的長(zhǎng)度完成的無字證明為( )
a + b 2 ≥ ab ( a > 0 , b > 0 ) | |
a + b 2 ≤ a 2 + b 2 2 | 2 ab a + b ≤ ab |
【考點(diǎn)】運(yùn)用基本不等式比較大小.
【答案】C
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/12/7 15:0:1組卷:117引用:7難度:0.6
相似題
-
1.已知a1>1,a2>1,M=a1+a2-1,N=
,則M,N的大小關(guān)系為( )a1a2A.M<N B.M>N C.M=N D.不確定 發(fā)布:2024/7/8 8:0:10組卷:14引用:0難度:0.8 -
2.已知a>1,b>1,記M=
,N=1a+1b,則M與N的大小關(guān)系為( )1abA.M>N B.M=N C.M<N D.不確定 發(fā)布:2024/8/31 15:0:9組卷:61引用:4難度:0.7 -
3.已知a>1>c,則
與(1-a)(c-1)的大小關(guān)系是( )a-c2A. (1-a)(c-1)≥a-c2B. (1-a)(c-1)≤a-c2C. (1-a)(c-1)>a-c2D. (1-a)(c-1)<a-c2發(fā)布:2024/8/26 8:0:8組卷:20引用:1難度:0.7


