2023-2024學年遼寧省沈陽市重點高中市郊聯體高一（上）期中數學試卷

一．單項選擇題（本題共8小題，每小題5分，共40分。在每小題給出的選項中，只有一個選項符合題目要求）

• 1．已知集合

  A

  =

  {

  x

  |

  x

  -

  2

  x

  +

  3

  ≤

  0

  }

  ，

  B

  =

  {

  x

  |

  x

  ≤

  1

  }

  ，則A∩B=（　　）

  A．{x|-3≤x≤1}

  B．{x|-3≤x≤2}

  C．{x|-3＜x≤1}

  D．{x|-3＜x＜2}
  組卷：32引用：1難度：0.7

  解析

• 2．設a∈R，則“a＞9”是“

  1

  a

  ＜

  1

  9

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：121引用：4難度：0.5

  解析

• 3．已知函數f（x）=

  6

  x

  -x²，在下列區間中，一定包含f（x）零點的區間是（　　）

  A．（-2，-1）

  B．（0，1）

  C．（1，2）

  D．（2，+∞）
  組卷：138引用：2難度：0.7

  解析

• 4．已知函數y=f（x）的定義域是[-4，5]，則

  y

  =

  f

  （

  x

  -

  1

  ）

  x

  +

  2

  的定義域是（　　）

  A．[-2，4]

  B．[-2，6]

  C．（-2，4]

  D．（-2，6]
  組卷：220引用：3難度：0.7

  解析

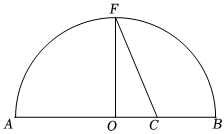• 5．《幾何原本》卷Ⅱ的幾何代數法成了后世西方數學家處理數學問題的重要依據．通過這一原理，很多代數的定理都能夠通過圓形實現證明，也稱之為無字證明現有如圖所示圖形，點F在半圓O上，點C在直徑AB上，且OF⊥AB，設AC=a,BC=b,可以直接通過比較線段OF與線段CF的長度完成的無字證明為（　　）

  A．a2+b2≥2ab（a＞0，b＞0）	B． a + b 2 ≥ ab （ a ＞ 0 ， b ＞ 0 ）
  C． a + b 2 ≤ a 2 + b 2 2 （a＞0，b＞0）	D． 2 ab a + b ≤ ab （a＞0，b＞0）
  組卷：117引用：7難度：0.6

  解析

• 6．關于x的不等式x²-mx-m＜0的解集為A，若[1，2]?A，則實數m的取值范圍為（　　）

  A．m＞0

  B． m ＞ 4 3

  C． m ≥ 1 2

  D． 1 2 ＜ m ＜ 4 3
  組卷：153引用：1難度：0.5

  解析

• 7．若函數

  f

  （

  x

  ）

  =

  （ a + 3 ） x - 3 ， x ＜ 1

  1 - a x + 1 ， x ≥ 1

  在R上單調遞增，則實數a的取值范圍是（　　）

  A． （ 0 ， 2 3 ]

  B．（0，+∞）

  C．（-3，+∞）

  D． （ - 3 ， 2 3 ]
  組卷：187引用：3難度：0.7

  解析

四，解答題

• 21．已知定義域在R上的函數f（x）滿足：f（x）=f（x-y）+f（y）+f（0），且當x＞0時，f（x）＜0．
  （1）證明函數f（x）在定義域上的單調性；
  （2）證明函數f（x）在定義域上奇偶性；
  （3）若?x∈（1，2），使得關于x的不等式f（x²-ax）+f（x-3）＞0成立，求實數a的取值范圍．
  組卷：137引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  ax

  +

  b

  x

  2

  +

  1

  是定義域為[-1，1]的奇函數，且f（1）=1．
  （1）求a,b的值，并判斷f（x）在[-1，1]上的單調性（不必證明）；
  （2）已知k為實數，函數g（x）=x²-2kx+4k+3，若對于任意x₁∈[-1，1]，總存在x₂∈（1，+∞），使得f（x₁）=g（x₂）成立，求k的取值范圍．
  組卷：68引用：1難度：0.4

  解析