如圖1，邊長為a cm的正方形硬紙板的4個角上剪去相同的小正方形，這樣可制作一個無蓋的長方體紙盒，設(shè)底面邊長為x cm.
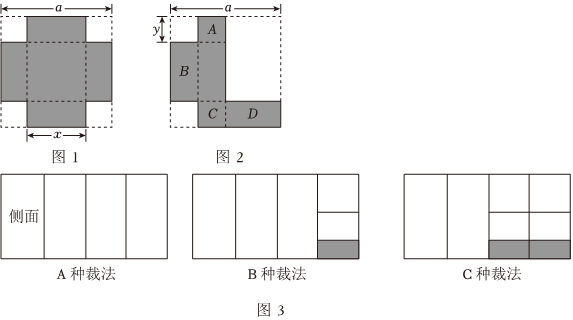
（1）這個紙盒的底面積是 x2x2cm2，高是 a-x2a-x2cm（用含a、x的代數(shù)式表示）．
（2）x的部分取值及相應(yīng)的紙盒容積如表所示：
a
-
x
2
a
-
x
2
| x/cm | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 紙盒容積/cm3 | m | 72 | n |
16
16
，n=81
2
81
2
②猜想：當(dāng)x逐漸增大時，紙盒容積的變化情況：
先隨著x的增大而增大，后隨著x的增大而減小
先隨著x的增大而增大，后隨著x的增大而減小
．（3）若將正方形硬紙板按圖2方式裁剪，亦可制作一個無蓋的長方體紙盒．
①若為該紙盒制作一個長方形蓋子，則該長方形的兩邊長分別是
y
y
cm,（a-2y）
（a-2y）
cm.（用含a、y的代數(shù)式表示）；②已知A，B，C，D四個面上分別標(biāo)有整式2（m+2），m,-3，6，且該紙盒的相對兩個面上的整式的和相等，求m的值．
（4）為了便捷生產(chǎn)，該廠經(jīng)調(diào)整尺寸后使得圖2中A為正方形．現(xiàn)計劃用50張白板紙制作圖2型號的長方體有蓋的紙箱，如圖3，每張白板紙可以用三種方法剪裁，其中第一種裁法：一張白板紙裁成4個側(cè)面；第二種裁法：一張白板紙裁成3個側(cè)面與2個底面；第三種裁法：一張白板紙裁成2個側(cè)面與4個底面，且四個側(cè)面和兩個底面恰好能做成一個紙箱．設(shè)按第一種方法剪裁的有x張白板紙，按第二種方法剪裁的有y張白板紙．當(dāng)x,y滿足怎樣的數(shù)量關(guān)系時，制作該種型號的長方體紙箱的個數(shù)最多？最多可制作多少個？
（5）現(xiàn)用紙箱裝一批玻璃飾品，某個玻璃飾品的外形是簡單多面體，它的外表面是由三角形和八邊形兩種多邊形拼接而成，且有24個頂點(diǎn)，每個頂點(diǎn)處都有3條棱，求該多面體表面三角形和八邊形的個數(shù)．（已知多面體頂點(diǎn)數(shù)+面數(shù)-2=棱數(shù)）
【答案】x2；；16；；先隨著x的增大而增大，后隨著x的增大而減小；y；（a-2y）
a
-
x
2
81
2
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/24 16:0:8組卷：232引用：2難度：0.5
相似題
-
1．）圖①、圖②、圖③均為8×7的網(wǎng)格，每個小正方形的邊長為1，每個小正方形的頂點(diǎn)稱為格點(diǎn)，線段AB的端點(diǎn)均在格點(diǎn)上，按要求完成下列各題：
（1）在圖①中作菱形ABCD，使C、D兩點(diǎn)均在格點(diǎn)上；
（2）在圖②中作矩形ABMN，使其鄰邊長度的比值為2；
（3）在圖③中作平行四邊形ABEF，滿足tanF=2，且E、F兩點(diǎn)均在格點(diǎn)上．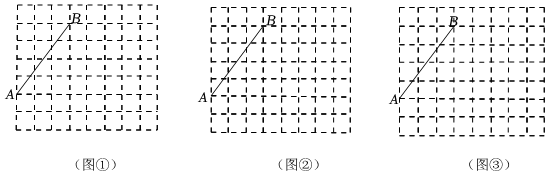
發(fā)布：2025/5/26 7:30:2組卷：143引用：1難度：0.5 -
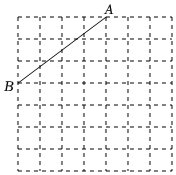2．如圖，方格紙中每個小正方形的邊長均為1個單位長度，線段AB端點(diǎn)在小正方形的頂點(diǎn)上．
（1）在方格紙中畫出一個以線段AB為一邊的平行四邊形ABCD（點(diǎn)C、點(diǎn)D在小正方形的頂點(diǎn)上），并且平行四邊形ABCD的面積為9．
（2）在方格紙中畫出以AB為斜邊的直角三角形ABE（點(diǎn)E在小正方形的頂點(diǎn)上），并且三角形ABE的面積為5，連接CE，請直接寫出線段CE的長．發(fā)布：2025/5/26 8:0:5組卷：14引用：1難度：0.5 -
3．如圖是由小正方形組成的8×8網(wǎng)格，每個小正方形邊長都是1，每個小正方形的頂點(diǎn)叫做格點(diǎn)，僅用無刻度的直尺完成畫圖，畫圖過程用虛線表示．
（1）在圖1中，先在邊AB上畫點(diǎn)F，使BF=3AF，再在邊BD上畫點(diǎn)G，使S△FBG=S△ABD；916
（2）在圖2中，在邊AD上面點(diǎn)H，使CH⊥BD，再在直線CH上取一點(diǎn)P，使AP+BP的值最小．
發(fā)布：2025/5/26 7:0:2組卷：160引用：1難度：0.5