在正方形ABCD中，AB=2，點E是BC邊的中點，連接DE，延長EC至點F，使得EF=DE，過點F作FG⊥DE，分別交CD、AB于N、G兩點，連接CM、EG、EN，下列正確的是
①②④
①②④
．（填序號）
①tan∠GFB=
1
2
；②MN=NC；③
CM
EG
=
1
2
；④S_{四邊形GBEM}=
5
+
1
2
．

【答案】①②④

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/23 11:0:1組卷：329引用：2難度：0.1

相似題

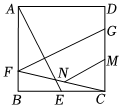1．如圖，點E為正方形ABCD的邊BC的中點，連接AE，點F、G分別為AB、CD上的點，連接FG，CF，取CG、CF的中點M、N，連接MN，已知正方形的邊長為4，若FG⊥AE，則MN的長為
．
發布：2025/5/23 17:30:1組卷：326引用：2難度：0.5
解析
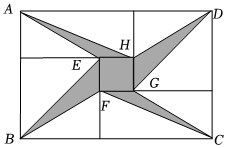2．如圖所示，將兩張相同的矩形紙片和三張不同的正方形紙片按如圖方式不重疊地放置在矩形ABCD內若知道圖中陰影部分的面積之和，則一定能求出（　　）
A．△AEH和△CFG的面積之差 B．△DHG和△BEF的面積之和
C．△BEF和△CFG的面積之和 D．△AEH和△BEF的面積之和
發布：2025/5/23 19:0:2組卷：350引用：2難度：0.5
解析
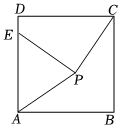3．如圖，點E在正方形ABCD的AD邊上，P為該正方形內一點，PA=PC=PE．請完成下列問題：
（1）若∠APE=70°，則∠PCD=
；
（2）若
DE
AE
=
1
4
，則
PA
AB
的值為
．
發布：2025/5/23 17:30:1組卷：167引用：3難度：0.5
解析

相關試卷

A．△AEH和△CFG的面積之差	B．△DHG和△BEF的面積之和
C．△BEF和△CFG的面積之和	D．△AEH和△BEF的面積之和

在正方形ABCD中，AB=2，點E是BC邊的中點，連接DE，延長EC至點F，使得EF=DE，過點F作FG⊥DE，分別交CD、AB于N、G兩點，連接CM、EG、EN，下列正確的是 ①②④①②④．（填序號）①tan∠GFB=12；②MN=NC；③CMEG=12；④S四邊形GBEM=5+12．