【問題呈現】如圖1，∠AOB=90°，OA=4，OB=5，點P在半徑為2的⊙O上，求12AP+BP的最小值．
【問題解決】小明是這樣做的：如圖2，在OA上取一點C使得OC=1，這樣可得OCOP=12=OPOA，又因為∠COP=∠POA，所以可得△COP∽△POA，所以CPAP=OPOA=12，得CP=12AP所以12AP+BP=CP+BP．又因為CP+BP≥CB=OC2+OB2，所以12AP+BP最小值為 2626．
【思路點撥】小明通過構造相似形（圖3），將12AP轉化成CP，再利用“兩點之間線段最短”求出CP+BP的最小值．
【嘗試應用】如圖4，∠AOB=60°，OA=10，OB=9，點P是半徑為6的⊙O上一動點，求AP+23BP的最小值．
【能力提升】如圖5，∠ABC=120°，BA=BC=8，點D為平面內一點且BD=3CD，連接AD，則△ABD面積的最大值為 12+18312+183．
1
2
AP
+
BP
OC
OP
=
1
2
=
OP
OA
CP
AP
=
OP
OA
=
1
2
CP
=
1
2
AP
1
2
AP
+
BP
=
CP
+
BP
CP
+
BP
≥
CB
=
O
C
2
+
O
B
2
1
2
AP
+
BP
26
26
1
2
AP
AP
+
2
3
BP
3
3
【考點】圓的綜合題．
【答案】；12+18
26
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：341引用：1難度：0.1
相似題
-
1．如圖1，直線l：y=-
x+b與x軸交于點A（4，0），與y軸交于點B，點C是線段OA上一動點（0＜AC＜34）．以點A為圓心，AC長為半徑作⊙A交x軸于另一點D，交線段AB于點E，連接OE并延長交⊙A于點F．165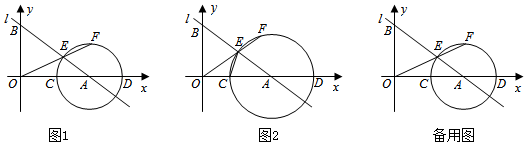
（1）求直線l的函數表達式和tan∠BAO的值；
（2）如圖2，連接CE，當CE=EF時，
①求證：△OCE∽△OEA；
②求點E的坐標；
（3）當點C在線段OA上運動時，求OE?EF的最大值．發布：2025/6/20 11:30:2組卷：5310引用：10難度：0.1 -
2．已知到直線l的距離等于a的所有點的集合是與直線l平行且距離為a的兩條直線l1、l2（如圖①）．
（1）在圖②的平面直角坐標系中，畫出到直線y=x+2的距離為1的所有點的集合的圖形．并寫出該圖形與y軸交點的坐標．2
（2）試探討在以坐標原點O為圓心，r為半徑的圓上，到直線y=x+2的距離為1的點的個數與r的關系．2
（3）如圖③，若以坐標原點O為圓心，2為半徑的圓上只有兩個點到直線y=x+b的距離為1，則b的取值范圍為 ．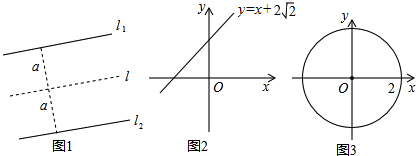
發布：2025/6/21 6:0:2組卷：516引用：9難度：0.5 -
3．已知：△ABC內接于⊙O，AB=AC，過B作BE⊥AC于點E，交⊙O于F，連CF．
（1）如圖1，求證：BE=FC+EE；
（2）如圖2，過B作BH⊥AF垂足為H，交AC于點G，求證：BG=BC；
（3）如圖3，在（2）的條件下，連接CH，若CH∥AB，CE=1，求AB的長．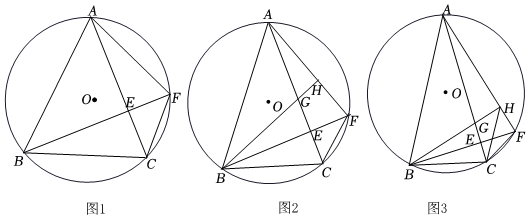
發布：2025/6/20 10:30:1組卷：14引用：1難度：0.2