當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省宿遷市宿城區(qū)青華中學九年級（下）開學數(shù)學試卷（A卷）

發(fā)布：2024/4/20 14:35:0

一、選擇題（本大題有8小題，每小題3分，共24分．在每小題所給出的四個選項中，只有一項是符合題目要求的，請將正確選項前的字母代號填涂在答題紙上．）

1．如果3x=4y（y≠0），那么下列比例式中成立的是（　　）
A．
x
3
=
y
4
B．
x
4
=
y
3
C．
x
y
=
3
4
D．
x
3
=
4
y
組卷：453引用：6難度：0.7
解析
2．二次函數(shù)y=x²-2x+3的圖象的頂點坐標是（　　）
A．（1，2） B．（1，6） C．（-1，6） D．（-1，2）
組卷：689引用：13難度：0.9
解析
3．如圖，在Rt△ABC中，∠C=90°，已知sinA=
3
4
，則cosB的值為（　　）
A．
7
4
B．
3
4
C．
3
5
D．
4
5
組卷：505引用：4難度：0.7
解析
4．若關于x的一元二次方程x²+2x+k=0有兩個不相等的實數(shù)根，則實數(shù)k的取值范圍是（　　）
A．k＞1 B．k=1 C．k＜1 D．k≤1
組卷：248引用：3難度：0.6
解析
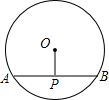5．如圖，在半徑為5的⊙O中，弦AB=6，OP⊥AB，垂足為點P，則OP的長為（　　）
A．3 B．2.5 C．4 D．3.5
組卷：3733引用：15難度：0.7
解析
6．設A（1，y₁），B（-2，y₂）是拋物線y=-（x+1）²+a上的兩點，則y₁、y₂的大小關系為（　　）
A．y₁＜y₂ B．y₁＞y₂ C．y₁≤y₂ D．y₁≥y₂
組卷：157引用：8難度：0.8
解析
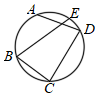7．如圖，點A、B、C、D、E在⊙O上，
?
AE
的度數(shù)為60°，則∠B+∠D的度數(shù)是（　　）
A．180° B．120° C．100° D．150°
組卷：1198引用：8難度：0.6
解析
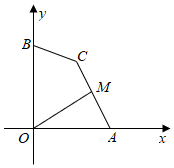8．如圖，點A，B的坐標分別為A（2，0），B（0，2），點C為坐標平面內一點，BC=1，點M為線段AC的中點，連接OM，則OM的最大值為（　　）
A．
2
+1 B．
2
+
1
2
C．2
2
+1 D．2
2
-
1
2
組卷：11879引用：53難度：0.4
解析

二、填空題（本大題有10小題，每小題3分，共30分．）

9．如果
cos
A
=
3
2
，那么銳角A的度數(shù)為
．
組卷：696引用：28難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題有10小題，共96分.解答時應寫出文字說明或演算步驟.）

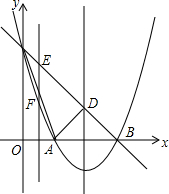27．如圖，拋物線y=ax²+bx+c（a≠0）的頂點坐標為（2，-1），并且與y軸交于點C（0，3），與x軸交于兩點A，B．
（1）求拋物線的表達式；
（2）設拋物線的對稱軸與直線BC交于點D，連接AC、AD，求△ACD的面積；
（3）點E為直線BC上一動點，過點E作y軸的平行線EF，與拋物線交于點F．問是否存在點E，使得以D、E、F為頂點的三角形與△BCO相似？若存在，求出點E的坐標；若不存在，請說明理由．
組卷：347引用：4難度：0.5
解析
28．【問題呈現(xiàn)】如圖1，∠AOB=90°，OA=4，OB=5，點P在半徑為2的⊙O上，求
1
2
AP
+
BP
的最小值．
【問題解決】小明是這樣做的：如圖2，在OA上取一點C使得OC=1，這樣可得
OC
OP
=
1
2
=
OP
OA
，又因為∠COP=∠POA，所以可得△COP∽△POA，所以
CP
AP
=
OP
OA
=
1
2
，得
CP
=
1
2
AP
所以
1
2
AP
+
BP
=
CP
+
BP
．又因為
CP
+
BP
≥
CB
=
O
C
2
+
O
B
2
，所以
1
2
AP
+
BP
最小值為
．
【思路點撥】小明通過構造相似形（圖3），將
1
2
AP
轉化成CP，再利用“兩點之間線段最短”求出CP+BP的最小值．
【嘗試應用】如圖4，∠AOB=60°，OA=10，OB=9，點P是半徑為6的⊙O上一動點，求
AP
+
2
3
BP
的最小值．
【能力提升】如圖5，∠ABC=120°，BA=BC=8，點D為平面內一點且BD=3CD，連接AD，則△ABD面積的最大值為
．
組卷：341引用：1難度：0.1
解析