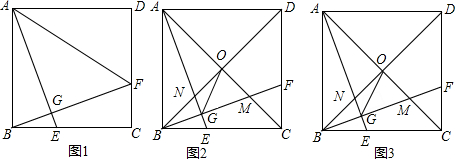
已知正方形ABCD中，點E在BC上，連接AE，過點B作BF⊥AE于點G，交CD于點F．
（1）如圖1，連接AF，若AB=4，BE=1，求AF的長；
（2）如圖2，連接BD，交AE于點N，連接AC，分別交BD、BF于點O、M，連接GO，求證：GO平分∠AGF；
（3）如圖3，在第（2）問的條件下，連接CG，若CG⊥GO，請直接寫出AGGC的值．
AG
GC
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：452引用：2難度：0.1
相似題
-
1．閱讀下面材料．
小炎遇到這個一個問題：如圖1，點E、F分別在正方形ABCD的邊BC、CD上，∠EAF=45°，連接EF，則EF=BE+DF，試說明理由．
小炎是這樣思考的：要想解決這個問題，首先應想辦法將這些分散的線段相對集中，她先嘗試了翻折、旋轉、平移的方法，最后發現線段AB、AD是共點并且相等的，于是找到解決問題的方法．她的方法是將△ABE繞著點A逆時針旋轉90°得到△ADG，再利用全等的知識解決這個問題（如圖2）．
參考小炎同學思考問題的方法，解決下列問題：
（1）寫出小炎的推理過程；
（2）如圖3，四邊形ABCD中，AB=AD，∠BAD=90°，點E、F分別在邊BC、CD上，∠EAF=45°，若∠B、∠D都不是直角，則當∠B與∠D滿足于 關系時，仍有EF=BE+DF；
（3）如圖4，在△ABC中，∠BAC=90°，AB=AC，點D、E均在邊BC上，且∠DAE=45°，若BD=1，EC=2，求DE的長．發布：2025/6/10 11:30:1組卷：291引用：2難度：0.2 -
2．如圖，矩形ABCD中，AB=4，AD=3，點E在折線BCD上運動，將AE繞點A順時針旋轉得到AF，旋轉角等于∠BAC，連接CF．
（1）當點E在BC上時，作FM⊥AC，垂足為M，求證：AM=AB；
（2）當AE=3時，求CF的長；2
（3）連接DF，點E從點B運動到點D的過程中，試探究DF的最小值．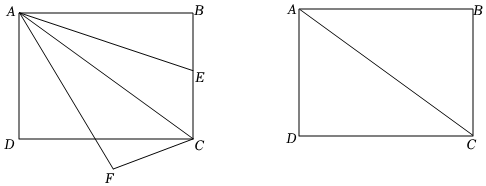
發布：2025/6/10 11:30:1組卷：3953引用：8難度：0.1 -
3．如圖，在矩形ABCD中，E是BC上一動點，將△ABE沿AE折疊后得到△AFE，點F在矩形ABCD內部，延長AF交CD于點G，AB=3，AD=4．
（1）如圖1，當∠DAG=30°時，求BE的長；
（2）如圖2，當點E是BC的中點時，求線段GC的長；
（3）如圖3，點E在運動過程中，當△CFE的周長最小時，直接寫出BE的長．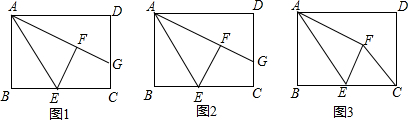
發布：2025/6/10 12:30:1組卷：1237引用：11難度：0.3