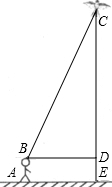
濟南的泉城廣場視野開闊，阻擋物少，成為不少市民放風箏的最佳場所．歷下區某校七年級（1）班的小明和小亮同學學習了“勾股定理”之后，為了測得圖中風箏的高度CE，他們進行了如下操作：
①測得BD的長為15米（注：BD⊥CE）；
②根據手中剩余線的長度計算出風箏線BC的長為25米；
③牽線放風箏的小明身高1.7米．
（1）求風箏的高度CE．
（2）過點D作DH⊥BC，垂足為H，求BH的長度．
【考點】勾股定理的應用．
【答案】（1）風箏的高度CE為21.7米．
（2）BH的長度為9米．
（2）BH的長度為9米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 19:0:2組卷：476引用：4難度：0.6
相似題
-
1．如圖，池塘邊有兩點A、B，點C是與BA方向成直角的AC方向上一點，測得CB=60m,AC=20m,則A，B兩點間的距離是（ ）發布：2025/6/8 1:0:1組卷：429引用：9難度：0.9 -
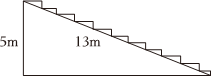2．如圖，要為一段高5米，長13米的樓梯鋪上紅地毯，至少需要紅地毯 米．發布：2025/6/8 0:30:1組卷：1688引用：27難度：0.9 -
3．有一個水池，水面是一個邊長為12尺的正方形，在水池正中央有一根蘆葦，它高出水面2尺，如果把這根蘆葦拉向水池一邊的中點，它的頂端恰好到達池邊的水面，則水的深度與這根蘆葦的長度分別是多少？發布：2025/6/8 0:0:1組卷：394引用：3難度：0.7