綜合與實踐
問題背景：
我們知道，三角形的中位線平行于三角形的第三邊，并且等于第三邊的一半，如何證明角形中位線定理呢？
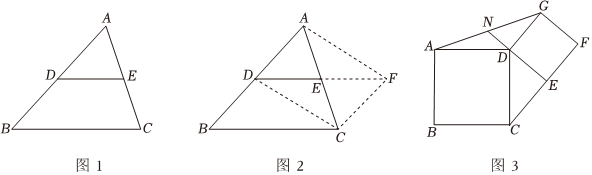
已知：如圖1，在△ABC中，D、E分別是AB、AC的中點．
求證：DE∥BC．DE=12BC．
思路分析：問題中既要證明兩條線段所在的直線平行，又要證明其中一條線段的長等于另一條線段長的一半，我們可以用“倍長法”將DE延長一倍：即延長DE到F．使得EF=DE，連接FC，DC，AF，通過證明四邊形ADCF與四邊形DBCF是平行四邊形從而得出最后結論．
問題解決：
（1）上述材料中“倍長法”體現的數學思想主要是 BB.（填入選項前的字母代號即可）
A．數形結合思想；B．轉化思想；C．分類討論思想；D．方程思想．
（2）請根據以上思路分析，完成”三角形中位線定理”的證明過程．
方法遷移：
（3）如圖3，四邊形ABCD和DEFG均為正方形，連接AG，CE，N是AG的中點，連接DN，已知線段DN=2，請求出線段CE的長．
DE
=
1
2
BC
【考點】四邊形綜合題．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/7 8:0:9組卷：271引用：3難度：0.2
相似題
-
1．如圖，在△ABC中，BD、CE分別為AC、AB邊上的中線，BD、CE交于點H，點G、F分別為HC、HB的中點，連接AH、DE、EF、FG、GD，其中HA=BC．
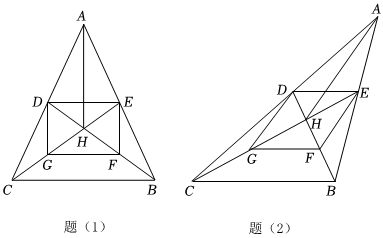
（1）當AC=AB時，求證：BD=CE；
（2）證明：四邊形DEFG為菱形；
（3）當猜想當AC、AB滿足怎樣的數量關系時，四邊形DEFG為正方形，并說明理由．發布：2025/6/8 5:30:2組卷：55引用：2難度：0.1 -
2．如圖，在平面直角坐標系中，點A的坐標為（6，0）．點Q從原點出發，沿著y軸正方向運動，動點P位于點A左側，且AP=2OQ，以OP，QP為鄰邊構造?POBQ，如圖1，設OQ=n.
（1）當點P運動到線段AO的中點時，求n的值及點B的坐標；
（2）?POBQ的面積能否等于4？若能，求出n的值；若不能，請說明理由；
（3）如圖2，點B關于原點的中心對稱點為點B′，連接AB′，OB′，當n為何值時，△AOB′為等腰三角形．（直接寫出答案）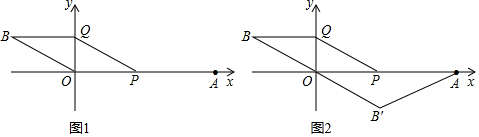
發布：2025/6/8 5:30:2組卷：375引用：5難度：0.2 -
3．如圖，在正方形ABCD中，點M在CD邊上，點N在正方形ABCD外部，且滿足∠CMN=90°，CM=MN．連接AN，CN，取AN的中點E，連接BE，AC，交于F點．
（1）①依題意補全圖形；
②求證：BE⊥AC．
（2）請探究線段BE，AD，CN所滿足的等量關系，并證明你的結論．
（3）設AB=1，若點M沿著線段CD從點C運動到點D，則在該運動過程中，線段EN所掃過的面積為（直接寫出答案）．發布：2025/6/8 6:30:2組卷：577引用：8難度：0.1