【問題情境】
課外興趣小組活動時，老師提出了如下問題：
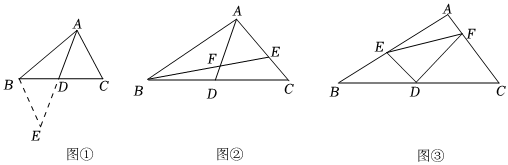
如圖①，△ABC中，若AB=8，AC=6，求BC邊上的中線AD的取值范圍．
小明在組內經過合作交流，得到了如下的解決方法：延長AD至點E，使DE=AD，連接BE．
請根據小明的方法思考：
（1）由已知和作圖能得到△ADC≌△EDB，依據是 AA．
A．SAS；B．SSS；C．AAS；D．HL
由“三角形的三邊關系”可求得AD的取值范圍是 1＜AD＜71＜AD＜7．
【初步運用】
（2）如圖②，AD是△ABC的中線，BE交AC于E，交AD于F，且AE=EF．若EF=4，EC=3，求線段BF的長．
【靈活運用】
（3）如圖③，在△ABC中，∠A=90°，D為BC中點，DE⊥DF，DE交AB于點E，DF交AC于點F，連接EF．試猜想線段BE．CF．EF三者之間的數量關系，并證明你的結論．
【考點】三角形綜合題．
【答案】A；1＜AD＜7
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：187引用：3難度：0.1
相似題
-
1．如圖，△ABC中，CA=CB、∠ACB=α，過點B作直線l∥AC，D為線段AB上一動點，連接CD，將射線DC繞點D順時針旋轉α，交直線l于點E．
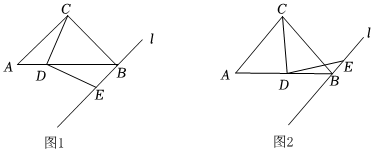
（1）如圖1，當α=90°時，線段CD和ED的數量關系是 ．
（2）如圖2，當0°＜α＜180°時，（1）中的結論是否仍然成立？若成立，請僅就圖2的情形給出證明；若不成立，請說明理由．
（3）若α=120°，AC=，當△DEB為直角三角形時，請直接寫出線段DE的長．3發布：2025/5/24 1:30:2組卷：55引用：1難度：0.1 -
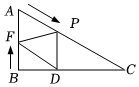2．如圖，在Rt△ABC?中，∠ABC=90°，∠C=30°，AB=9cm?，動點P?從點A?開始以2cm/s?的速度向點C?運動，動點F?從點B?開始以1cm/s?的速度向點A?運動，兩點同時運動，同時停止，運動時間為t（s）?．
（1）當t?為何值時，△PAF?是等邊三角形？
（2）當t?為何值時，△PAF?是直角三角形？
（3）過點P?作PD⊥BC?于點D?，連接DF?．
①求證：四邊形AFDP?是平行四邊形；
②當t?為何值時，△PDC?的面積是△ABC?面積的一半．發布：2025/5/24 1:0:1組卷：283引用：3難度：0.3 -
3．在一次數學興趣小組活動中，小明將兩個形狀相同，大小不同的三角板AOB和三角板DEB放置在平面直角坐標系中，點O（0，0），A（0，3），∠ABO=30°，BE=3．
（Ⅰ）如圖①，求點D的坐標；
（Ⅱ）如圖②，小明同學將三角板DEB繞點B按順時針方向旋轉一周．
①若點O，E，D在同一條直線上，求點D到x軸的距離；
②連接DO，取DO的中點G，在旋轉過程中，點G到直線AB的距離的最大值是 （直接寫出結果即可）．發布：2025/5/24 1:0:1組卷：573引用：2難度：0.3