如圖1，AB是⊙O的直徑，BC是⊙O的切線，點(diǎn)D是直徑AB右側(cè)半圓上一點(diǎn)，過點(diǎn)D作DE⊥AB于點(diǎn)E，連結(jié)AC交DE于點(diǎn)P．
（1）求證：AC?PE=AP?BC．
（2）連結(jié)OC、AD，若AD∥OC，求證：PE=PD．
（3）如圖2，連結(jié)CD，若CD是⊙O的切線，求證：PE=PD．
【考點(diǎn)】圓的綜合題．
【答案】（1）證明見解答；
（2）證明見解答；
（3）證明見解答．
（2）證明見解答；
（3）證明見解答．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：544引用：1難度：0.3
相似題
-
1．[問題提出]
（1）如圖1，已知線段AB=4，點(diǎn)C是一個動點(diǎn)，且點(diǎn)C到點(diǎn)B的距離為2，則線段AC長度的最大值是 ；
[問題探究]
（2）如圖2，以正方形ABCD的邊CD為直徑作半圓O，E為半圓O上一動點(diǎn)，若正方形的邊長為2，求AE長度的最大值；
[問題解決]
（3）如圖3，某植物園有一塊三角形花地ABC，經(jīng)測量，AC=20米，BC=120米，∠ACB=30°，BC下方有一塊空地（空地足夠大），為了增加綠化面積，管理員計(jì)劃在BC下方找一點(diǎn)P，將該花地?cái)U(kuò)建為四邊形ABPC，擴(kuò)建后沿AP修一條小路，以便游客觀賞．考慮植物園的整體布局，擴(kuò)建部分△BPC需滿足∠BPC=60°．為容納更多游客，要求小路AP的長度盡可能長，問修建的觀賞小路AP的長度是否存在最大值？若存在，求出AP的最大長度；若不存在，請說明理由．3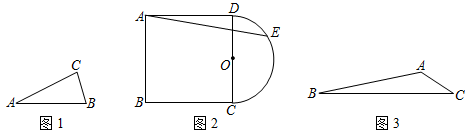
發(fā)布：2025/5/23 10:30:1組卷：904引用：8難度：0.2 -
2．問題研究．
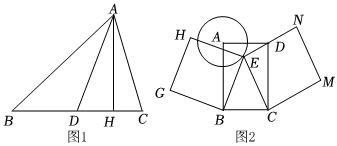
如圖1，AD是△ABC的中線，AH是BC邊上的高．
（1）當(dāng)AH=6，CD=5，DH=3時，AB=．
（2）求證：AB2+AC2=2AD2+2BD2．
問題解決
（3）某地為打造元宵節(jié)燈展景觀，需按如下要求設(shè)計(jì)一批燈展造型．如圖2，矩形ABCD是造型框架，以頂點(diǎn)A為圓心懸掛圓形燈架（⊙A），以B，C為頂點(diǎn)釘兩個正方形展板（正方形BEHG和正方形CENM），接合點(diǎn)點(diǎn)E恰好在⊙A上．若AD=1.4m,AB=2.4m,⊙A的半徑為0.7m,求兩個正方形展板面積和的最小值．發(fā)布：2025/5/23 10:30:1組卷：128引用：3難度：0.1 -
3．如圖，已知O是△ABC邊AB上的一點(diǎn)，以O(shè)為圓心、OB為半徑的⊙O與邊AC相切于點(diǎn)D，且BC=CD，連接OC，交⊙O于點(diǎn)E，連接BE并延長，交AC于點(diǎn)F．
（1）求證：BC是⊙O切線；
（2）求證：OA?AB=AD?AC；
（3）若，求EO的長．AC=10，tan∠BAC=43發(fā)布：2025/5/23 11:30:2組卷：738引用：4難度：0.3
相關(guān)試卷