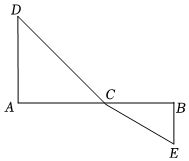
探究：如圖所示，C為線段AB上一動點，分別過點A，點B作AD⊥AB，BE⊥AB，分別連接CD，CE．已知AD=4，BE=2，AB=8．設AC=x.
（1）CD=⎷42+x2⎷42+x2，CE=⎷（8-x）2+22⎷（8-x）2+22（用含x的代數(shù)式表示）；
（2）探究點D，C，E處于何種位置時，CD+CE的值最小，并求出其最小值；
（3）根據(jù)（2）中的探究結果，請構圖并求出代數(shù)式√x2+1+⎷（12-x）2+16的最小值．（要求畫出示意圖）
⎷
4
2
+
x
2
⎷
4
2
+
x
2
⎷
（
8
-
x
）
2
+
2
2
⎷
（
8
-
x
）
2
+
2
2
√
x
2
+
1
+
⎷
（
12
-
x
）
2
+
16
【考點】軸對稱-最短路線問題．
【答案】；
⎷
4
2
+
x
2
⎷
（
8
-
x
）
2
+
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/8/4 8:0:9組卷：690引用：8難度：0.4
相似題
-
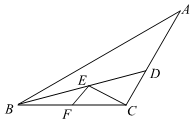1．在△ABC中，AC=BC=8，∠ACB=120°，BD平分∠ABC交AC于點D，點E、F分別是線段BD，BC上的動點，則CE+EF的最小值是 ．發(fā)布：2025/6/1 20:0:1組卷：292引用：6難度：0.5 -
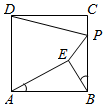2．如圖，已知正方形ABCD的邊長為2，點E是正方形內(nèi)部一點，連接EA，EB滿足∠EAB=∠EBC，點P是BC邊上一動點，連接PD，PE．則PD+PE長度的最小值為（ ）發(fā)布：2025/6/1 16:30:1組卷：720引用：3難度：0.5 -
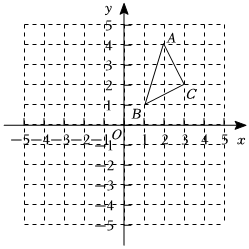3．在邊長為1個單位長度的正方形網(wǎng)格中建立如圖所示的平面直角坐標系，△ABC的頂點都在格點上（小正方形的頂點稱為格點），請解答下列問題：
（1）畫出△ABC關于y軸對稱的△A1B1C1，并寫出點C1為（ ，）
（2）求出△ABC的面積為 ．
（3）在y軸上存在一點P使得AP+BP最小，在圖中畫出點P的位置，則P點的坐標為（ ，），AP+BP的最小值為 ．發(fā)布：2025/6/1 19:0:6組卷：238引用：4難度：0.6